Question

For any two sets A and B, prove that:
1. $A\cup B=B\cup A$ [Commutative law for the union of sets]
2. $A\cap B=B\cap A$ [Commutative law for the intersection of sets]

Answer 1

Hint:First of all take an element $x\in A\cup B$ and $x\in A\cap B$ in each of the proofs respectively. Now, by the definition of intersection and union of sets, prove that $x\in B\cup A$ and $x\in B\cap A$. From this, prove that $A\cap B\subset B\cap A$ and vice versa. From this and its converse, prove the desired result. Similarly, do for the other one as well.

Complete step-by-step answer:
Here, for any two sets A and B, prove that
1. $A\cup B=B\cup A$ [Commutative law for the union of sets]
2. $A\cap B=B\cap A$ [Commutative law for the intersection of sets]
Let us prove that $A\cup B=B\cup A$. Let x be an element in the set $A\cup B$. So, we can write
$x\in A\cup B$
We know that $A\cup B$ constitute elements in A or B or in both. So, if $x\in A\cup B$, then $x\in A$ or $x\in B$. We can also say that as $x\in B$ or $x\in A$, so, $x\in B\cup A$.
So, from $x\in A\cup B$, we get, $x\in B\cup A$. From this, we can say that $A\cup B$ is a subset of $B\cup A$
So, we get,
$A\cup B\subset B\cup A.....\left( i \right)$
Let us consider the reverse of the commutative law of union of two sets that is $B\cup A=A\cup B$
Let $x\in B\cup A$. If $x\in B\cup A$, then $x\in B$ or $x\in A$. We can also say that $x\in A$ or $x\in B$. So, $x\in A\cup B$.
So, from $x\in B\cup A$, we get, $x\in A\cup B$. From this, we can say that $B\cup A$ is a subset of $A\cup B$. So, we get,
$B\cup A\subset A\cup B.....\left( ii \right)$
We know that when x is a subset of y and y is a subset of x, then x = y. So, from equation (i) and (ii), we get,
$A\cup B=B\cup A$
Hence, we have proved the commutative law from the union of sets.

Now let us prove that $A\cap B=B\cap A$. Let x be an element in $A\cap B$. So, we can write $x\in A\cap B$. We know that $A\cap B$ constitute elements that are in set A as well as B.
So if, $x\in A\cap B$, then $x\in A$ and $x\in B$. Also, we can say that $x\in B$ and $x\in A$. So, we get, $x\in B\cap A$. From $x\in A\cap B$, we get $x\in B\cap A$. So, we can say that $A\cap B$ is a subset of $B\cap A$. Therefore, we get,
$A\cap B\subset B\cap A....\left( iii \right)$
Now, let us consider the reverse of commutative law for the intersection of two sets that is
$B\cap A=A\cap B$
Let $x\in B\cap A$, then $x\in B$ , and $x\in A$. We can say that $x\in A$ and $x\in B$. So, we get, $x\in A\cap B$. From $x\in B\cap A$, we get, $x\in A\cap B$. So, we can say that $B\cap A$ is a subset of $A\cap B$. Therefore, we get,
$B\cap A\subset A\cap B....\left( iv \right)$
We know that when x is a subset of y and y is a subset of x, then x = y.
So, from equation (iii) and (iv), we get,
$A\cap B=B\cap A$
Hence, we have proved that the commutative law for the intersection of two sets.

Note: Students can also verify their relationship by Venn Diagram as follows:

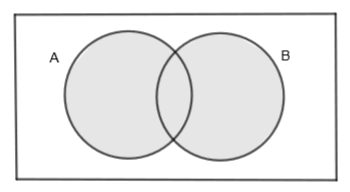
In the above diagram, we can write the shaded portion as $A\cup B$ or $B\cup A$. So, we get, $A\cup B=B\cup A$.

In the above diagram, we can write the shaded portion as $A\cap B$ or $B\cap A$. So, we get, $A\cap B=B\cap A$