Question

For any two non-zero vectors a and b, $(ab+ba).(ab-ba)$ is

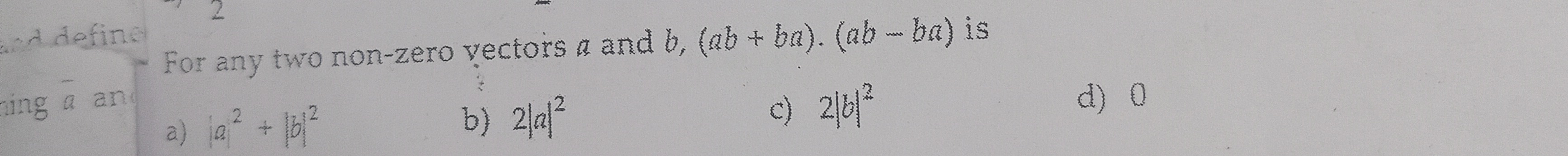
• A. $|a|^2 + |b|^2$
• B. $2|a|^2$
• C. $2|b|^2$
• D. 0

Answer 1

Answer: (D)

0

Answer 2

Given the expression:

$(ab+ba) \cdot (ab-ba)$

Notice that if we assume "ab" denotes a product (whether dot product or cross product), then in both cases the operation is commutative or anti-commutative:

1. Case 1 (Dot Product):
   Since the dot product is commutative, we have:

   $ab+ba = 2(a \cdot b)$ and $ab-ba = 0$.

   Hence,

   $(ab+ba) \cdot (ab-ba) = 2(a \cdot b) \cdot 0 = 0$.

2. Case 2 (Cross Product):
   The cross product is anti-commutative, i.e., $\mathbf{a \times b} = - (\mathbf{b \times a})$. So,

   $ab+ba = \mathbf{a \times b} + \mathbf{b \times a} = 0$,

   and

   $ab-ba = \mathbf{a \times b} - \mathbf{b \times a} = 2\,\mathbf{a \times b}$.

   Thus,

   $(ab+ba) \cdot (ab-ba) = 0 \cdot 2\,\mathbf{a \times b} = 0$.

In either interpretation, the answer is 0.