Question

For any sets A and B prove that:
(a) $A\cap B'=\phi \Rightarrow A\subset B$
(b) $A'\cup B=U\Rightarrow A\subset B$

Answer 1

Hint:First we will draw the Venn diagram and we will also give the definitions of the required terms, and then we will use this to prove the above two statements. We will also take some values of A, B and U, to verify the above relations.

Complete step-by-step answer:
Let’s first write some definitions of terms.
Universal set: The set containing all objects or elements and of which all other sets are subsets.
Complement of a set: Complement of a set A, denoted by A c, is the set of all elements that belongs to the universal set but does not belong to set A.
Union: The union (denoted by $\cup$ ) of a collection of sets is the set of all elements in the collection. It is one of the fundamental operations through which sets can be combined and related to each other.
Intersection: The intersection of two sets has only the elements common to both sets. If an element is in just one set it is not part of the intersection. The symbol is an upside down $\cap$ .

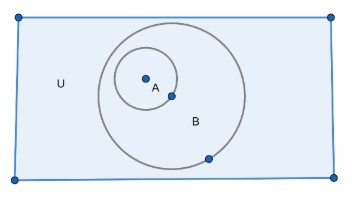
Let’s start solving each part one by one.
For part (a):
First we will draw the Venn diagram of B’

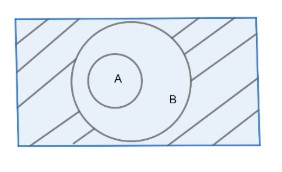
From the above diagram and the definition of intersection we can see that $A\cap B'$ is a null set.
Therefore,
$A\cap B'=\phi$
And for this to be true we need $A\subset B$ as shown above.
Hence proved (a).
Now let’s take an example to see if it’s true or not.
Let A = {1, 2}, B = {1, 2, 3}, U = {1, 2, 3, 4}
B’ will be the elements in U that are not in B.
B’ = {4}
Now we will find $A\cap B'$,
A = {1, 2} and B’ = {4} , there is no common element in these two.
Therefore,
$A\cap B'$ = $\phi$
Hence, by taking an example we have proved.
For part (b):
Let’s first look at the Venn diagram of A’

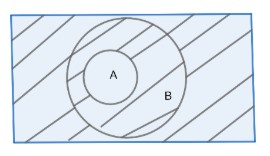
The shaded part is A’
Similarly from the above diagram and definition of union we can see that $A'\cup B=U$
As it covers the whole universal set.
The part that is left by A’ is covered by B and for this to be true $A\subset B$ must also be true.
Similarly we can take values of A, U and B and show that it is true.
Hence proved (b).
Let’s take an example to see if it’s true or not.
Let A = {1, 2}, B = {1, 2, 3}, U = {1, 2, 3, 4}
A’ will be the elements in U that are not in A.
Therefore,
A’ = { 3, 4 }
Now we are going to find $A'\cup B$ ,
A’ = { 3, 4 } and B = {1, 2, 3}, now taking all the elements of these two we get,
$A'\cup B$ = { 1, 2, 3, 4 } = U
Hence, by taking an example we have proved.
And hence both the statements have been proved.

Note: The definitions that we have used to solve this question must be kept in mind, and one can take any values of A, B, and U to check the above two relations.