Question
Question: For any positive integer $n$, Let $f_n : [0, \infty) \rightarrow R$ as $f_n(x) = \sum_{i=1}^{n} \tan...
For any positive integer n, Let fn:[0,∞)→R as fn(x)=∑i=1ntan−1(1+(x+i)(x+i−1)1)∀x∈[0,∞) then find value of ∑i=15tan2(fi(0)).
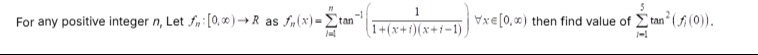
55
Solution
The given function is fn(x)=∑i=1ntan−1(1+(x+i)(x+i−1)1).
We can simplify the term inside the tan−1 function. Let y=x+i−1. Then x+i=y+1. The term is tan−1(1+y(y+1)1).
Using the identity tan−1A−tan−1B=tan−1(1+ABA−B), we can write 1+y(y+1)1 as 1+y(y+1)(y+1)−y.
So, tan−1(1+y(y+1)1)=tan−1(y+1)−tan−1(y).
Substituting back y=x+i−1, we get tan−1(1+(x+i)(x+i−1)1)=tan−1((x+i−1)+1)−tan−1(x+i−1)=tan−1(x+i)−tan−1(x+i−1).
Now, we can write fn(x) as a telescoping sum: fn(x)=∑i=1n[tan−1(x+i)−tan−1(x+i−1)] fn(x)=(tan−1(x+1)−tan−1(x))+(tan−1(x+2)−tan−1(x+1))+⋯+(tan−1(x+n)−tan−1(x+n−1)) All intermediate terms cancel out, leaving: fn(x)=tan−1(x+n)−tan−1(x).
We need to find the value of ∑i=15tan2(fi(0)). First, let's find fi(0). Substitute x=0 into the expression for fn(x): fn(0)=tan−1(0+n)−tan−1(0)=tan−1(n)−0=tan−1(n). So, fi(0)=tan−1(i) for i=1,2,3,4,5.
Next, we need to calculate tan2(fi(0)): tan2(fi(0))=tan2(tan−1(i)). For any real number k, tan(tan−1(k))=k. So, tan2(tan−1(i))=(i)2=i2.
Finally, we need to calculate the sum ∑i=15tan2(fi(0)): ∑i=15tan2(fi(0))=∑i=15i2. This is the sum of the squares of the first 5 positive integers: ∑i=15i2=12+22+32+42+52=1+4+9+16+25=55.
The value of the sum is 55.
