Question

For any four points P,Q, R, S $\left| {\overrightarrow {PQ} \times \overrightarrow {RS} - \overrightarrow {QR} \times \overrightarrow {PS} + \overrightarrow {PS} + \overrightarrow {RP} \times \overrightarrow {QS} } \right|$ is equal to 4 times the area of the triangle.
A. PQR
B. QRS
C. PRS
D. PQS

Answer 1

In order to solve the above problem, we will assume these four points are points of a parallelogram and since in parallelogram the parallel sides are equal in length, therefore the vectors which are parallel have the same magnitude but opposite direction. We will solve the above problem step by step using these concepts

Complete step-by-step answer:

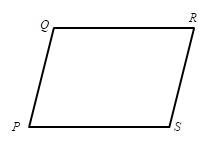
Let P, Q, R, S be the four points of a parallelogram
Therefore
$\overrightarrow {PQ} = a$
$\overrightarrow {RS} = - a$
Since PQ and RS are parallel to each other, therefore they have the same magnitude and for the direction the negative sign is shown in RS
Similarly QR and OS are parallel to each other,
$\overrightarrow {QR} = b$
$\overrightarrow {PS} = b\,\,and\,\,\,\,\overrightarrow {SP} = - b\,\,$
The given equation is
$\left| {\overrightarrow {PQ} \times \overrightarrow {RS} - \overrightarrow {QR} \times \overrightarrow {PS} + \overrightarrow {PS} + \overrightarrow {RP} \times \overrightarrow {QS} } \right|$
Substituting the value of the vectors from above

$$= \left| {a \times \left( { - a} \right) - b \times b + b + \left( {a - b} \right) \times \left( {a - b} \right)} \right|\sin E \\\ = | - {a^2} - {b^2} + {a^2} + {b^2} - 2ab|\sin E \\\ = - 2ab\sin E \\\$$

$A = 4 \times \left( {\dfrac{{ - 1}}{2}\left| {a \times b} \right|} \right) \\\ A = 4 \times area\,of\,QRS \\\$

Note: In order to solve these types of problems, remember the concept of that the area of the triangle is equal to 1/2 times the magnitude of the cross product of the 2 vectors that form the triangle with the vectors continuous. The area of the parallelogram is equal to= magnitude of the cross product of the 2 vectors that are joined together from head to tail.