Solveeit Logo
Login

Question

Question: For any curve \[xy = {c^2}\] the subnormal at any point varies as 1) \[{x^2}\] 2) \[{x^3}\] 3)...

For any curve xy=c2xy = {c^2} the subnormal at any point varies as

  1. x2{x^2}
  2. x3{x^3}
  3. y2{y^2}
  4. y3{y^3}
Explanation

Solution

Here in this question we have to determine the subnormal, so first we have to find the derivative of the given curve with respect to x and then by using the formula y×dydxy \times \dfrac{{dy}}{{dx}} we determining the subnormal variation. Then we choose an appropriate option in the question.

Complete step by step answer:
We usually know about the tangent and normal. So first we know about the subtangent and subnormal
Let y = f (x) be the curve that is differentiable at a point P. Let the tangent and normal at P(x, y) to the curve meet at the x-axis at points T and N. M is the projection of P on the x-axis. In the figure below,
PT is the length of the tangent
PN is the length of the normal
TM is the length of subtangent
MN is the length of the subnormal

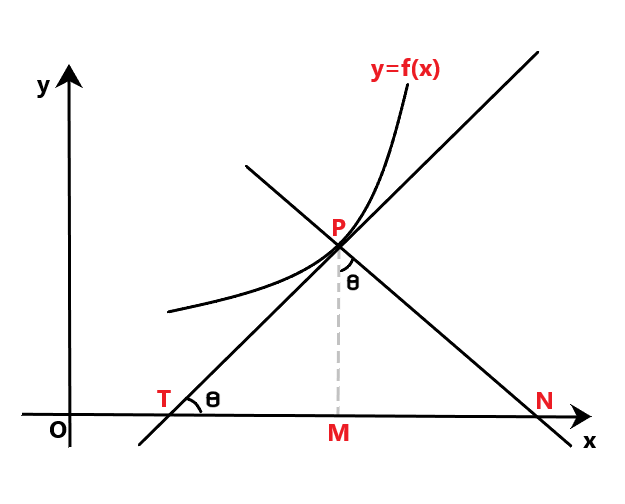
Now consider the given question, the curve is xy=c2xy = {c^2}---- (1)
The equation can be written as
⇒y=c2x\Rightarrow y = \dfrac{{{c^2}}}{x} ----(2)
On differentiating the equation (2) with respect to x we have
⇒dydx=−c2x2\Rightarrow \dfrac{{dy}}{{dx}} = - \dfrac{{{c^2}}}{{{x^2}}}
The formula to determine the subnormal is y×dydxy \times \dfrac{{dy}}{{dx}}, so we have
⇒y×−c2x2\Rightarrow y \times - \dfrac{{{c^2}}}{{{x^2}}}-------(3)
Consider the equation (2) y=c2xy = \dfrac{{{c^2}}}{x}, this can be written as x=c2yx = \dfrac{{{c^2}}}{y}----- (4)
On substituting the equation (4) in the equation (3) we have
⇒y×−c2(c2y)2\Rightarrow y \times - \dfrac{{{c^2}}}{{{{\left( {\dfrac{{{c^2}}}{y}} \right)}^2}}}
On squaring the denominator term we have
⇒y×−c2c4y2\Rightarrow y \times - \dfrac{{{c^2}}}{{\dfrac{{{c^4}}}{{{y^2}}}}}
Taking the reciprocal we have
⇒y×c2×y2c4\Rightarrow y \times {c^2} \times \dfrac{{{y^2}}}{{{c^4}}}
On simplifying we have
⇒y3c2\Rightarrow \dfrac{{{y^3}}}{{{c^2}}}
where c represents the constant. Therefore for any curve xy=c2xy = {c^2} the subnormal at any point varies as y3{y^3}

So, the correct answer is “Option 4”.

Note: To determine the length of tangent, normal, subtangent and subnormal of a curve we have to know the formula and it is given as follows
1. The length of tangent = ∣y∣1+(dxdy)2|y|\sqrt {1 + {{\left( {\dfrac{{dx}}{{dy}}} \right)}^2}}
2. The length of normal = ∣y×dxdy∣\left| {y \times \dfrac{{dx}}{{dy}}} \right|
3. The length of subtangent = ∣y∣1+(dydx)2|y|\sqrt {1 + {{\left( {\dfrac{{dy}}{{dx}}} \right)}^2}}
4.The length of subnormal = ∣y×dydx∣\left| {y \times \dfrac{{dy}}{{dx}}} \right|