Question

For any complex number $z, \overline{z} = (\frac{1}{z})$ if and only if

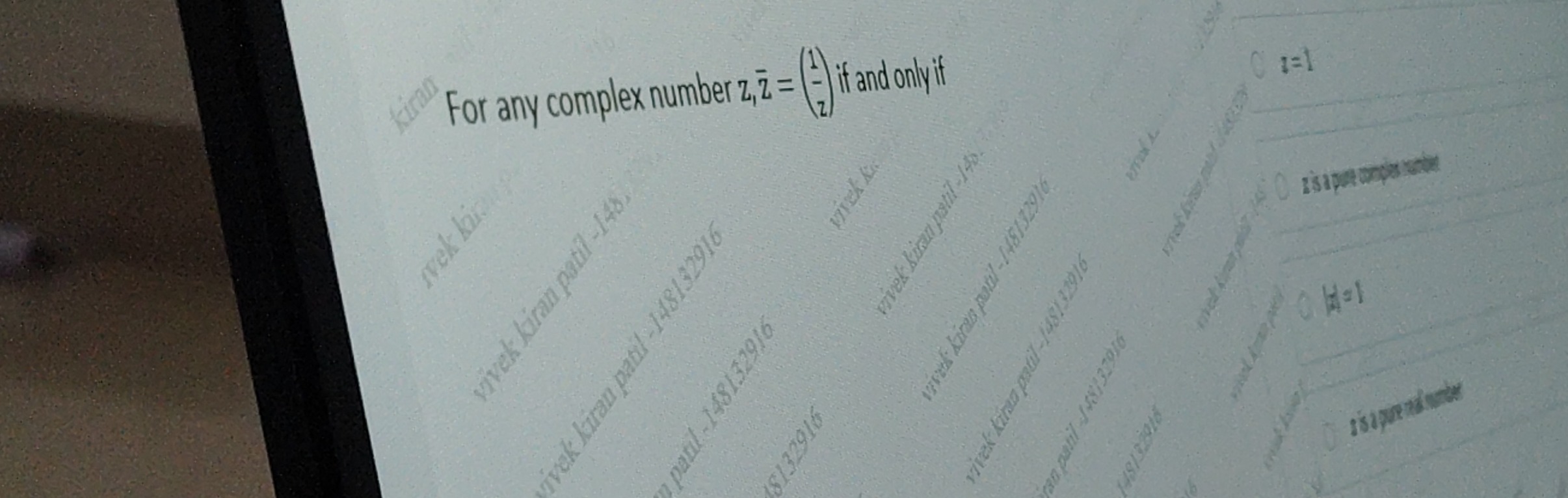
• A. $z = 1$
• B. $z$ is a pure complex number
• C. $|z| = 1$
• D. $z$ is a pure real number

Answer 1

Answer: (C)

$|z| = 1$

Answer 2

Given the condition $\overline{z} = \frac{1}{z}$.
Multiply both sides by $z$:
$z \overline{z} = 1$
We know that for any complex number $z$, $z \overline{z} = |z|^2$.
Substituting this into the equation:
$|z|^2 = 1$
Taking the square root of both sides (since $|z|$ is always non-negative):
$|z| = 1$