Question

For an orbital in $B^{+4}$ radial function is : $R(r) = \frac{1}{\sqrt[3]{Z}}(\frac{Z}{a_0})^{\frac{5}{2}}\frac{\sqrt{6}}{9}(4-\sigma)\sigma e^{-\sigma/2}$

where $\sigma=\frac{2Zr}{na_0}$ and $a_0=0.529 \mathring{A}; Z = \text{atomic number}, r = \text{radial distance from nucleus.}$

The radial node of orbital is at distance ......... $\mathring{A}$ from nucleus.

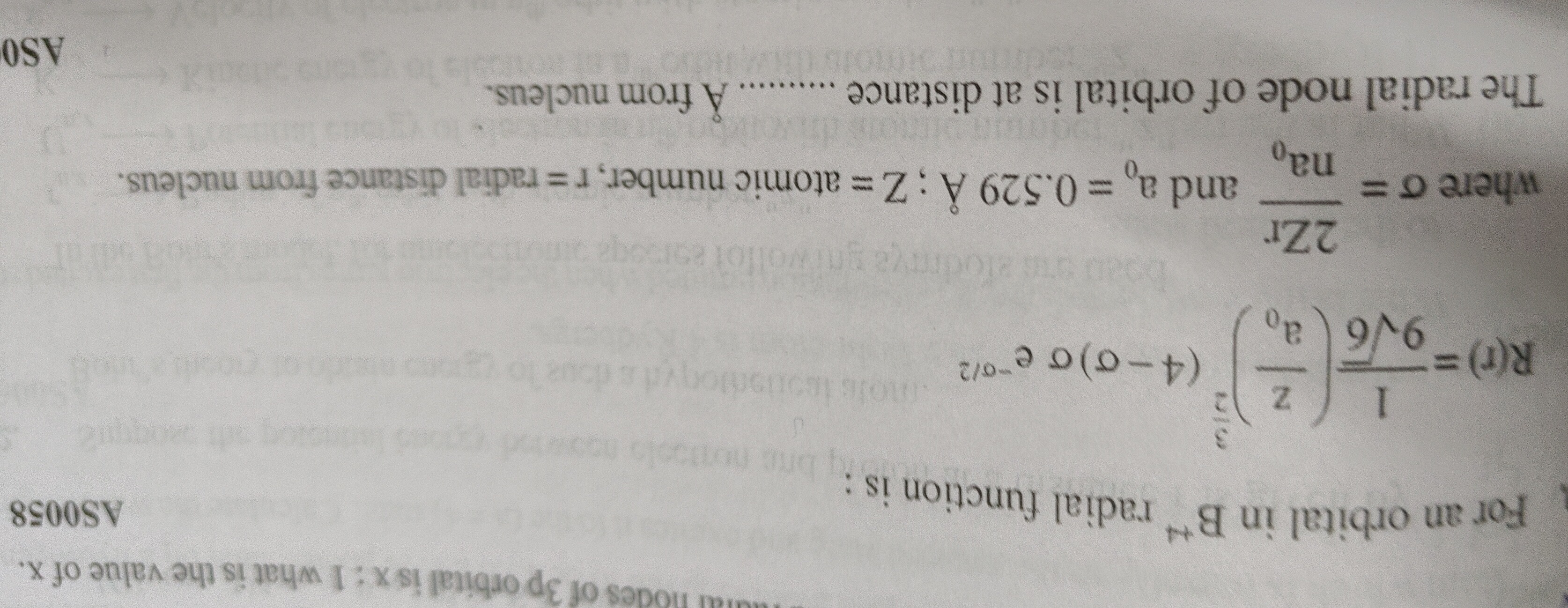
Answer 1

0.6348

Answer 2

The given radial function is proportional to $\sigma(4-\sigma)e^{-\sigma/2}$. Comparing with the general form $\sigma^l L_{n-l-1}^{2l+1}(\sigma)e^{-\sigma/2}$, we deduce $l=1$ and $L_{n-2}^3(\sigma) \propto (4-\sigma)$, which implies $n-2=1$, so $n=3$. The orbital is $3p$. The number of radial nodes is $n-l-1 = 1$. Nodes occur where the radial function is zero for $r>0$. The roots of $\sigma(4-\sigma)$ are $\sigma=0$ and $\sigma=4$. Thus, the radial node is at $\sigma=4$. For $B^{+4}$, $Z=5$ and $n=3$. Substituting $\sigma=4$ into $\sigma=\frac{2Zr}{na_0}$ gives $4=\frac{2 \times 5 \times r}{3a_0}$, yielding $r=1.2a_0$. With $a_0=0.529 \mathring{A}$, $r=0.6348 \mathring{A}$.