Question
Question: For an npn transistor \( {R_{out}} = 1.2 \times {10^5}\Omega \) , \( {R_{in}} = 6000\Omega \) , \( \...
For an npn transistor Rout=1.2×105Ω , Rin=6000Ω , β=50 . It is connected to amplify an input signal in active mode in common emitter configuration. The input signal is
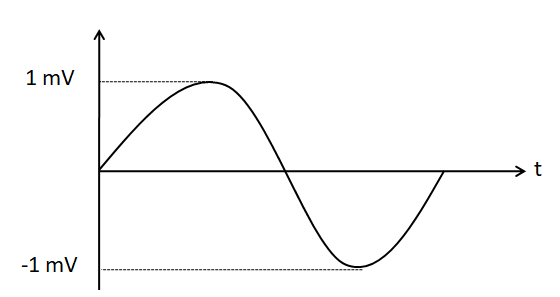
The output signal looks like
(A) 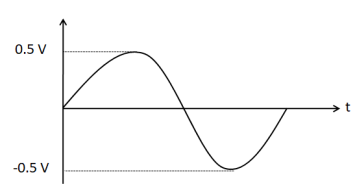
(B) 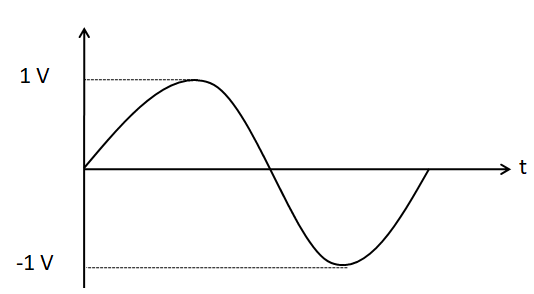
(C) 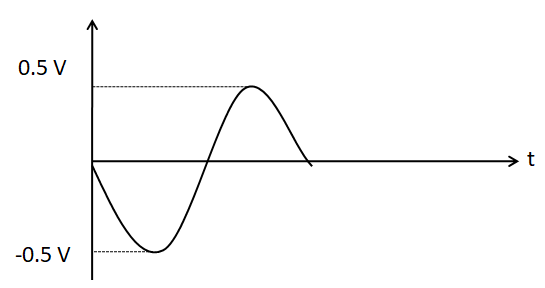
(D) 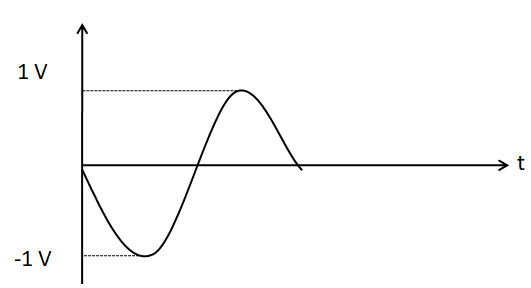
Solution
Hint
To answer this question, we have to use the formula of the voltage gain in the case of an npn transistor in active mode in common emitter configuration. The input voltage can be determined from the waveform of the input signal given. From the value of the voltage gain, we can determine the output voltage and hence predict the shape of the output signal.
Formula Used: The formula used to solve this question is
v=−βRinRout
Here v is the voltage gain, β is the current amplification factor or the current gain, Rout is the output resistance and Rin is the input resistance.
Complete step by step answer
According to the question, the current gain β=50 , Rout=1.2×105Ω , and Rin=6000Ω
We know that for an npn transistor in the common emitter configuration in the active mode, the voltage gain is given by
v=−βRinRout
Substituting the values, we get
v=−50×60001.2×105
v=−50×20
On solving, we get
v=−1000 (1)
We know that the voltage gain is equal to the ratio of the output voltage to the input voltage, that is,
v=VinVout (2)
From the waveform of the input signal given in the question, we can see that the amplitude of the input voltage is equal to 1mV . That is, Vin=1 mV
∴v=1 mVVout
Vout=v×(1 mV)
Substituting from (1)
Vout=−1000×(1 mV)
Vout=−1V
Thus, the output voltage has the amplitude of 1V .
Hence, the options A and C are incorrect, as they do not have output voltage amplitude equal to 1V .
The negative sign in the expression of the voltage gain indicates a phase change of 180∘ from the input to the output. Therefore after being amplified, the input voltage is inverted. So, the output voltage waveform should look like
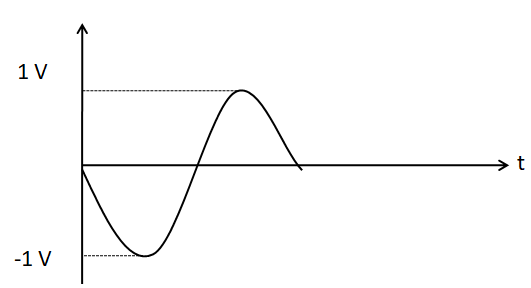
Hence, the correct answer is option D.
Note
Do not forget the negative sign present in the expression of the voltage gain. Always remember, the voltage is always inverted when a transistor is operated in the active mode in the common emitter configuration.
