Question

For an ideal gas, the value of ${{\left( \dfrac{dU}{dV} \right)}_{T}}$ is:
(A)- positive
(B)- zero
(C)- negative
(D)- interchangeable

Answer 1

Variation of internal energy (U) of a gas with volume at constant temperature is given by Joule’s law. It says that for an ideal gas, internal energy is a function of temperature only.

Complete step by step answer:
According to Joule’s law, the change of internal energy (U) of an ideal gas with volume (V) at a particular temperature (T) is zero. The term ${{\left( \dfrac{dU}{dV} \right)}_{T}}$ is called internal pressure.
It is mathematically given as
${{\left( \dfrac{dU}{dV} \right)}_{T}}=0$

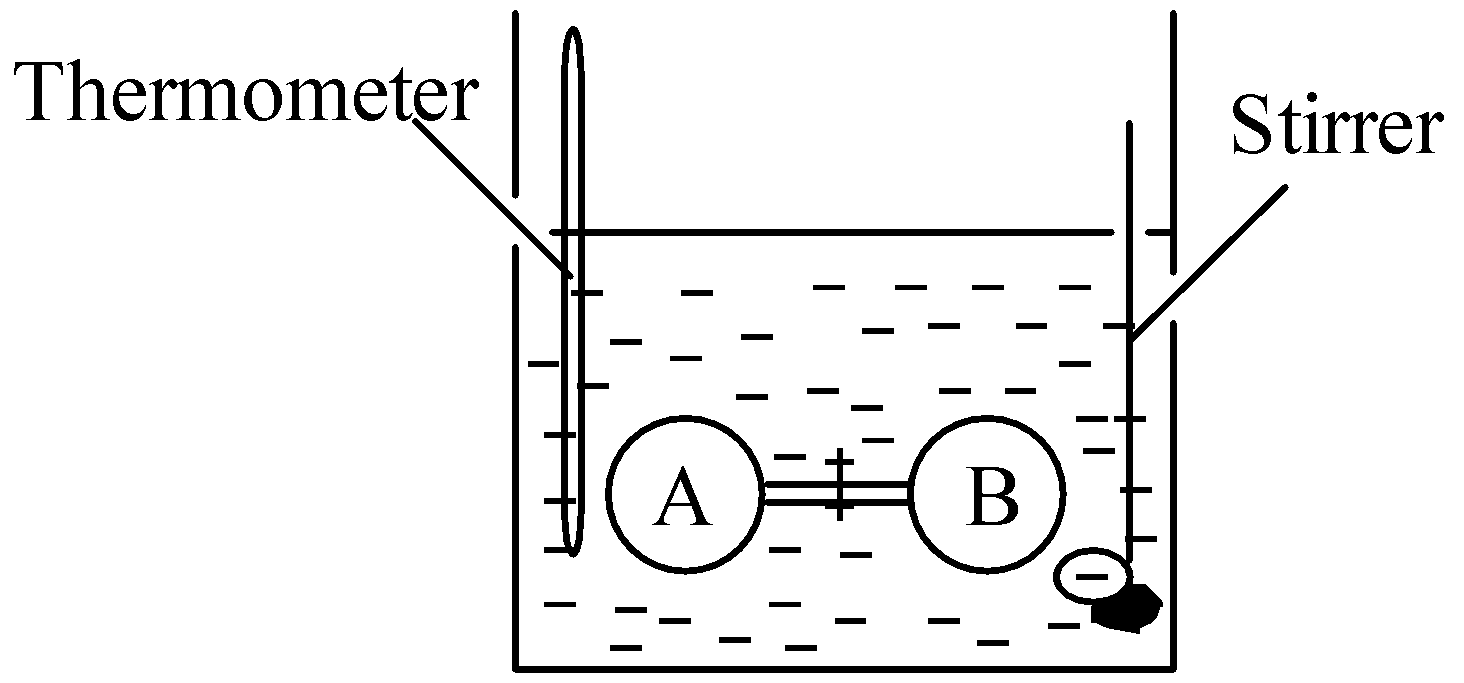
This conclusion was derived on the basis of the Joule experiment. Joule performed an experiment to find the internal pressure of a gas. The experimental setup is shown in figure below:

Consider internal energy as a function of temperature T and volume V.
$dU={{\left( \dfrac{\partial U}{\partial T} \right)}_{V}}dT+{{\left( \frac{\partial U}{\partial V} \right)}_{T}}dV$

In water bath, two bulbs, i.e. A and B were connected by stop cock. Bulb A was filled with air whereas bulb B was evacuated. The bulbs were allowed to come in thermal equilibrium with the surrounding water. The water was stirred and temperature was recorded. Now the stop cock was opened and the temperature was recorded again. No change in temperature was recorded.

From the first law of thermodynamics, $dU=dq+dW$.
We know that $dW=-{{P}_{oppo\sin g}}dV$. Now, as the gas was expanded into vacuum, no work was done during the expansion because, ${{P}_{oppo\sin g}}=0$.

Thus, $dW=0$. During the expansion of the gas, it exchanged no heat, i.e.$dq=0$.
Substituting $dW-0$ and $dq=0$ in the mathematical expression for first law of thermodynamic, we get
$dU=0$
Now, we can write
${{\left( \dfrac{\partial U}{\partial T} \right)}_{V}}dT+{{\left( \dfrac{\partial U}{\partial V} \right)}_{T}}dV=0$

But we know that change in temperature, i.e. $dT=0$. Therefore,
${{\left( \dfrac{\partial U}{\partial V} \right)}_{T}}dV=0$
Now during expansion, change in volume cannot be zero, i.e. $dV\ne 0$. Hence, we get
${{\left( \dfrac{\partial U}{\partial V} \right)}_{T}}=0$
So, the correct answer is “Option B”.

Note: Internal energy is volume independent; this statement is only valid for ideal gases. In ideal gases, the forces of attraction between the gaseous molecules are zero. If the question was about the internal pressure of real gases, the answer would be positive, i.e. option (A).