Solveeit Logo
Login

Question

Question: For all values of \( A\& B \) ,Prove that \( \cos (A - B) = \cos A.\cos B - \operatorname{Sin} A.\op...

For all values of A&BA\& B ,Prove that cos⁡(A−B)=cos⁡A.cos⁡B−Sin⁡A.Sin⁡B\cos (A - B) = \cos A.\cos B - \operatorname{Sin} A.\operatorname{Sin} B

Explanation

Solution

Hint : To calculate the value we first construct a circle and mark the points with respect to sine and cosine. Then, we will compare the two chords which subtend equal angles. Then we will be able to prove the equation by solving the equation.

Complete step by step solution:

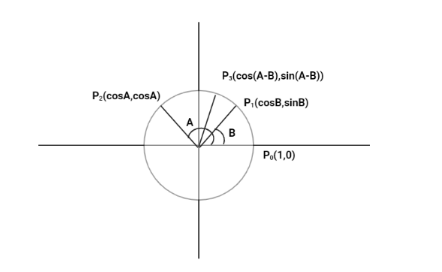
Equal chords of a circle subtends equal angle at the centre.
Hence, P1P2{P_1}{P_2} chord and P0P3{P_0}{P_3} chord are equal as they both angles are the same at centre that is A−BA - B .
P0P3=P1P2 ⇒(cos(A−B)−1)2+(sin(A−B)−0)2=(cos⁡A−cos⁡B)2+(sin⁡A−sin⁡B)2   {P_0}{P_3} = {P_1}{P_2} \\\ \Rightarrow \sqrt {{{(cos(A - B) - 1)}^2} + {{(sin(A - B) - 0)}^2}} = \sqrt {{{(\cos A - \cos B)}^2} + {{(\sin A - \sin B)}^2}} \;
(Using the distance formula)
Now, squaring both sides we will get,
(cos(A−B)−1)2+(sin(A−B)−0)2=(cos⁡A−cos⁡B)2+(sin⁡A−sin⁡B)2 Cos⁡2(A−B)+1−2cos⁡(A−B)+sin⁡2(A−B)=cos⁡2A+cos⁡2B−2cos⁡Acos⁡B+sin⁡2A+sin⁡2B+2sin⁡Asin⁡B   {(cos(A - B) - 1)^2} + {(sin(A - B) - 0)^2} = {(\cos A - \cos B)^2} + {(\sin A - \sin B)^2} \\\ {\operatorname{Cos} ^2}(A - B) + 1 - 2\cos (A - B) + {\sin ^2}(A - B) = {\cos ^2}A + {\cos ^2}B - 2\cos A\cos B + {\sin ^2}A + {\sin ^2}B + 2\sin A\sin B \;
We know that sin⁡2θ+cos⁡2θ=1{\sin ^2}\theta + {\cos ^2}\theta = 1
Cos⁡2(A−B)+sin⁡2(A−B)+1−2cos⁡(A−B)=cos⁡2A+sin⁡2A+cos⁡2B+sin⁡2B−2cos⁡Acos⁡B+2sin⁡Asin⁡B ⇒1+1−2cos⁡(A−B)=1+1−2cos⁡Acos⁡B+2sin⁡Asin⁡B ⇒2−2cos⁡(A−B)=2−2cos⁡Acos⁡B+2sin⁡Asin⁡B ⇒−2cos⁡(A−B)=−2(cos⁡Acos⁡B−sin⁡Asin⁡B)   \\{ {\operatorname{Cos} ^2}(A - B) + {\sin ^2}(A - B)\\} + 1 - 2\cos (A - B) = \\{ {\cos ^2}A + {\sin ^2}A\\} + \\{ {\cos ^2}B + {\sin ^2}B\\} - 2\cos A\cos B + 2\sin A\sin B \\\ \Rightarrow 1 + 1 - 2\cos (A - B) = 1 + 1 - 2\cos A\cos B + 2\sin A\sin B \\\ \Rightarrow {2} - 2\cos (A - B) ={2} - 2\cos A\cos B + 2\sin A\sin B \\\ \Rightarrow -{2}\cos (A - B) = -{2}(\cos A\cos B - \sin A\sin B) \;
Hence, cos(A−B)=cos⁡A.cos⁡B−sin⁡A.sin⁡Bcos(A - B) = \cos A.\cos B - \sin A.\sin B
Therefore, for all values of A&BA\& B cos⁡(A−B)=cos⁡A.cos⁡B−Sin⁡A.Sin⁡B\cos (A - B) = \cos A.\cos B - \operatorname{Sin} A.\operatorname{Sin} B

Note : Using cos⁡(A−B)\cos (A - B) and cos⁡(A+B)\cos (A + B) we can further derive many other formulas like cos⁡2x\cos 2x, cos⁡3x\cos 3x, sin⁡2x\sin 2x and sin⁡3x\sin 3x. All these identities can be derived in the same manner as we did in the above question.