Solveeit Logo
Login

Question

Question: For all the complex numbers \[{{z}_{1}},{{z}_{2}}\] satisfying \[\left| {{z}_{1}} \right|=32\] and \...

For all the complex numbers z1,z2{{z}_{1}},{{z}_{2}} satisfying ∣z1∣=32\left| {{z}_{1}} \right|=32 and ∣z2−12−5i∣=13,\left| {{z}_{2}}-12-5i \right|=13, the minimum value of ∣z2−z1∣\left| {{z}_{2}}-{{z}_{1}} \right| is
(a) 2
(b) 6
(c) 12
(d) 16

Explanation

Solution

Hint : To solve the given question, we will first find out what complex numbers are. Now, we will try to represent the equations given in the question into the complex plane. For this, we will make use of the fact that the general equation of the circle in a complex pane is ∣z−z1∣=r\left| z-{{z}_{1}} \right|=r where z1{{z}_{1}} is the coordinate of the centre and r is the radius of the circle. Then, the minimum value of ∣z1−z2∣\left| {{z}_{1}}-{{z}_{2}} \right| will be equal to the difference between the radius of the outer circle and the diameter of the inner circle.

Complete step by step solution :
Before we solve the given question, we must know what complex numbers are. A complex number is a number that can be represented in the form of a + ib, where a and b are real numbers and i represents the imaginary unit, satisfying the equation i2=−1.{{i}^{2}}=-1. Now, we know that if a circle is present in a complex plane, then the equation of a circle will be
∣z−z1∣=r\left| z-{{z}_{1}} \right|=r
where z1{{z}_{1}} is the coordinate of the centre and r is the radius of the circle. With the help of this concept, we can find the radius and centre of the circles given in the question.
Now, we can write ∣z1∣=32\left| {{z}_{1}} \right|=32 as ∣z1−0∣=32.\left| {{z}_{1}}-0 \right|=32. This means that the coordinates of the centre will be (0, 0) and its radius will be 32.
Similarly, we can write ∣z2−12−5i∣=13\left| {{z}_{2}}-12-5i \right|=13 as ∣z2−(12+5i)∣=13.\left| {{z}_{2}}-\left( 12+5i \right) \right|=13. This means that the coordinates will be (12, 5) and its radius will be 13. Also, this circle passes through the centre because when we put z2=0{{z}_{2}}=0 in the above equation, LHS = RHS.
Now, we will draw the rough sketch of both these circles in a complex plane.

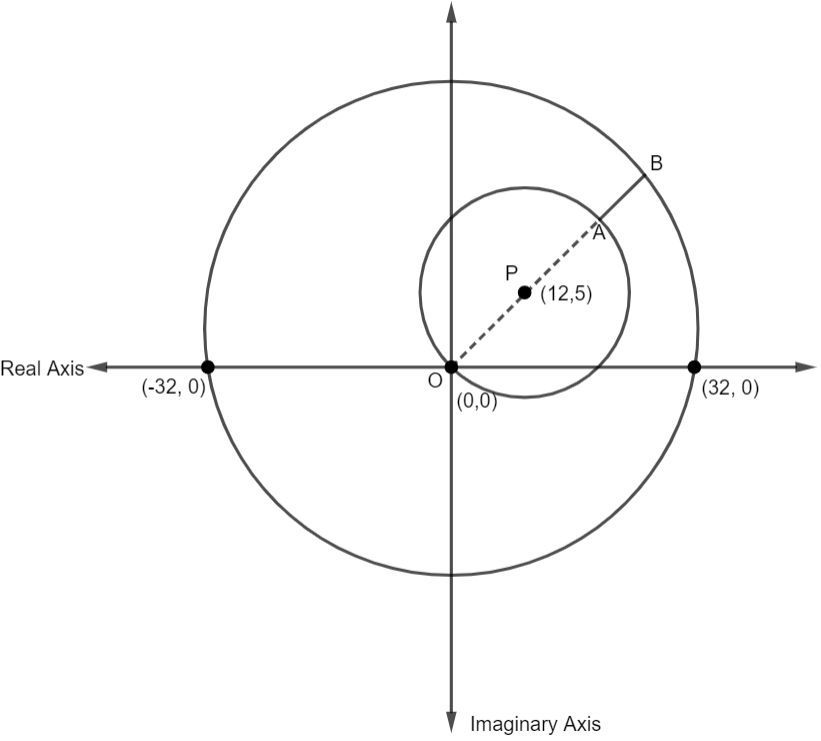
From the above figure, we can see that the minimum value of ∣z1−z2∣\left| {{z}_{1}}-{{z}_{2}} \right| will be equal to the length AB. Now, P is the centre of the circle ∣z2−12−5i∣=B\left| {{z}_{2}}-12-5i \right|=B and OA is its diameter. OB is the radius of the circle ∣z1∣=13.\left| {{z}_{1}} \right|=13. Thus, we can say that,
∣z2−z1∣=AB=OB−OA\left| {{z}_{2}}-{{z}_{1}} \right|=AB=OB-OA
⇒∣z2−z1∣=OB−2(OP)\Rightarrow \left| {{z}_{2}}-{{z}_{1}} \right|=OB-2\left( OP \right)
⇒∣z2−z1∣=32−2(13)\Rightarrow \left| {{z}_{2}}-{{z}_{1}} \right|=32-2\left( 13 \right)
⇒∣z2−z1∣=32−26\Rightarrow \left| {{z}_{2}}-{{z}_{1}} \right|=32-26
⇒∣z2−z1∣=6\Rightarrow \left| {{z}_{2}}-{{z}_{1}} \right|=6
Hence, option (b) is the right answer.

Note : The alternate method of solving the above question is shown below. If A and B are two complex numbers then we have,
∣∣A∣−∣B∣∣≤∣A−B∣\left| \left| A \right|-\left| B \right| \right|\le \left| A-B \right|
Thus, we can say that,
∣∣z2−12−5i∣−∣z1∣∣≤∣z2−z1−12−5i∣\left| \left| {{z}_{2}}-12-5i \right|-\left| {{z}_{1}} \right| \right|\le \left| {{z}_{2}}-{{z}_{1}}-12-5i \right|
⇒∣19∣≤∣z2−z1−12−5i∣\Rightarrow \left| 19 \right|\le \left| {{z}_{2}}-{{z}_{1}}-12-5i \right|
⇒19≤∣z2−z1−12−5i∣......(i)\Rightarrow 19\le \left| {{z}_{2}}-{{z}_{1}}-12-5i \right|......\left( i \right)
∣∣z2−z1∣−∣12+5i∣∣≤∣z2−z1−12−5i∣\left| \left| {{z}_{2}}-{{z}_{1}} \right|-\left| 12+5i \right| \right|\le \left| {{z}_{2}}-{{z}_{1}}-12-5i \right|
⇒∣∣z2−z1∣−(12)2+(5)2∣≤∣z2−z1−12−5i∣\Rightarrow \left| \left| {{z}_{2}}-{{z}_{1}} \right|-\sqrt{{{\left( 12 \right)}^{2}}+{{\left( 5 \right)}^{2}}} \right|\le \left| {{z}_{2}}-{{z}_{1}}-12-5i \right|
⇒∣∣z2−z1∣−13∣≤∣z2−z1−12−5i∣......(ii)\Rightarrow \left| \left| {{z}_{2}}-{{z}_{1}} \right|-13 \right|\le \left| {{z}_{2}}-{{z}_{1}}-12-5i \right|......\left( ii \right)
From (i) and (ii),
⇒∣∣z2−z1∣−13∣=19\Rightarrow \left| \left| {{z}_{2}}-{{z}_{1}} \right|-13 \right|=19
⇒∣z2−z1∣−13=±19\Rightarrow \left| {{z}_{2}}-{{z}_{1}} \right|-13=\pm 19
⇒∣z2−z1∣=∣13+19∣ or ∣z2−z1∣=∣13−19∣\Rightarrow \left| {{z}_{2}}-{{z}_{1}} \right|=\left| 13+19 \right|\text{ or }\left| {{z}_{2}}-{{z}_{1}} \right|=\left| 13-19 \right|
⇒∣z2−z1∣=32 or ∣z2−z1∣=∣−6∣\Rightarrow \left| {{z}_{2}}-{{z}_{1}} \right|=32\text{ or }\left| {{z}_{2}}-{{z}_{1}} \right|=\left| -6 \right|
⇒∣z2−z1∣=32 or ∣z2−z1∣=6\Rightarrow \left| {{z}_{2}}-{{z}_{1}} \right|=32\text{ or }\left| {{z}_{2}}-{{z}_{1}} \right|=6
Thus the minimum value of ∣z2−z1∣\left| {{z}_{2}}-{{z}_{1}} \right| is 6.