Question

For a uniform lamina ABCD, whose center is O.

& A){{\text{I}}_{\text{AC}}}=\sqrt{2}{{\text{I}}_{\text{EF}}} \\\ & B)\sqrt{2}{{\text{I}}_{\text{AC}}}={{\text{I}}_{\text{EF}}} \\\ & C){{\text{I}}_{\text{AC}}}={{\text{I}}_{\text{EF}}} \\\ & D){{\text{I}}_{\text{AC}}}=3{{\text{I}}_{\text{EF}}} \\\ \end{aligned}$$

Answer 1

We will assume 2 axes in which one is perpendicular to EF and one perpendicular to AC. Then we will use a perpendicular axis theorem for the given lamina by considering each axis as a particular case. By comparing the formed equations, we will deduce the relation between the given axes.

Formula used:
${{I}_{Z}}={{I}_{X}}+{{I}_{Y}}$

Complete step-by-step answer:
Let us understand what a perpendicular axis theorem is. It states that the moment of inertia of a planar lamina about an axis perpendicular to the plane of lamina is equal to the sum of the moments of inertia of the lamina about the two axes at right angles to each other. i.e.${{I}_{Z}}={{I}_{X}}+{{I}_{Y}}$.
Here, we will assume the given lamina ABCD is in XY plane. Then we will assume two axes E’F’ and A’C’ which are perpendicular to EF and AC respectively. We will draw a diagram indicating those.

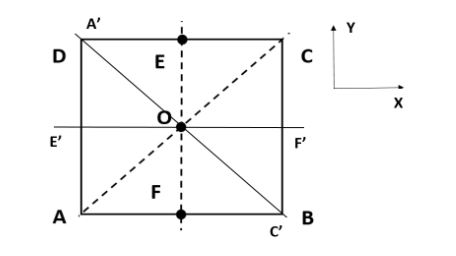
From this figure, by symmetry, we can understand that,
${{I}_{EF}}={{I}_{E'F'}}$ -- (1)
And ${{I}_{AC}}={{I}_{A'C'}}$ -- (2)
Now, we will apply a perpendicular axis theorem along the z- axis using the axes EF and E’F’.
${{I}_{Z}}={{I}_{E'F'}}+{{I}_{EF}}$
But using (1), the moment of inertia through z-axis will be,
$\Rightarrow {{I}_{Z}}=2{{I}_{EF}}$ --- (3)
Now, if we apply axis theorem along z- axis using the axes AC and A’C’,
${{I}_{Z}}={{I}_{A'C'}}+{{I}_{AC}}$
But using (2), the moment of inertia through z-axis will be,
$\Rightarrow {{I}_{Z}}=2{{I}_{AC}}$ --- (4)
Then, if we compare (3) and (4), they are equal.

& \Rightarrow 2{{I}_{EF}}=2{{I}_{AC}} \\\ & \Rightarrow {{I}_{EF}}={{I}_{AC}} \\\ \end{aligned}$$ Therefore, we found that $${{I}_{EF}}={{I}_{AC}}$$. **So, the correct answer is “Option C”.** **Note:** We can also solve this question by considering the moment of inertia of a square lamina which is given as $$\dfrac{m{{l}^{2}}}{6}$$. Then we will apply a perpendicular axes theorem in which moment of inertia of the axes at right angles will be equal. If we consider the axes through the diagonals of the lamina, it will also be the same. In this way also, we will get the moment of inertia of both given axes as same.