Question

- For $A \to B$, optical path is

A. $2\left( {a + b} \right)$
B. $2\left( {a - b} \right)$
C. $a + b$
D. $a - b$

Answer 1

The optical path in a certain medium is the product of distance travelled by the ray in that medium and refractive index of that medium. Use Snell’s law to determine the refractive index of the second medium. Assume the first medium to be air medium.

Formula used:
$OP = nd$
Here, n is the refractive index and d is the distance travelled by the light ray.

Complete step by step solution:
We assume the point at the boundary between two mediums where incident ray and refracted ray meet is O. Then we can draw the above diagram as below,

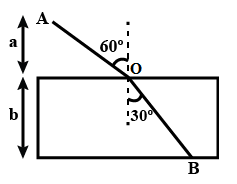
Now, the optical path of the above ray in both the mediums is,
$OP = {n_1}\left( {AO} \right) + {n_2}\left( {OB} \right)$
Here, ${n_1}$ is the refractive index of the medium from which the incident ray is travelling and ${n_2}$ is the refractive index of the medium from which the refracted ray is travelling.
Since the air has refractive index 1, we can write the above equation as follows,
$OP = \left( {AO} \right) + {n_2}\left( {OB} \right)$ …… (1)
From the above figure, we can write,
$\cos 60^\circ = \dfrac{a}{{AO}}$
$\Rightarrow AO = \dfrac{a}{{\cos 60^\circ }} = 2a$
Also, $\cos 30^\circ = \dfrac{b}{{OB}}$
$\Rightarrow OB = \dfrac{b}{{\cos 30^\circ }} = \dfrac{{2b}}{{\sqrt 3 }}$
Using Snell’s law, we can determine the refractive index of the second medium as follows,
$\left( 1 \right)\sin 60^\circ = {n_2}\sin 30^\circ$
$\Rightarrow {n_2} = \dfrac{{\sin 60^\circ }}{{\sin 30^\circ }}$
$\Rightarrow {n_2} = \sqrt 3$
Now, substituting $2a$ for AO, $\dfrac{{2b}}{{\sqrt 3 }}$for OB and $\sqrt 3$ for ${n_2}$ in equation (1), we get,
$OP = 2a + \sqrt 3 \left( {\dfrac{{2b}}{{\sqrt 3 }}} \right)$
$\Rightarrow OP = 2a + 2b$
$\Rightarrow OP = 2\left( {a + b} \right)$

Additional information:
The optical path length (OPL) is the product of the path length of the light ray and refractive index of the medium through which it is travelling. The difference in the path length is known as optical path difference (OPD).

Note:
While using Snell’s law, the incident angle is not the angle between incident ray and horizontal surface but it is the angle made by the incident ray with the normal. In this solution, we have assumed that the medium from which the incident rays are travelling is the air medium since it is not given in the question.