Question

For a series R-L-C circuit: (a) Voltage across L and C are differ by $\pi$ (b) Current through L and R are in same phase (c) Voltage across R and L differ by ${}^{\pi }/{}_{2}$ (d) Voltage across L and current through C are differ by ${}^{\pi }/{}_{2}$.

A. a, b, c
B. 2, 3, 4
C. c, d, a
D. All

Answer 1

Using the phase diagrams of the current and the voltage, it becomes easy to compare the phase difference between the voltages and the currents belonging to resistor, inductor and the capacitor.

Complete step by step answer:

Consider the phase diagrams of voltage and current.
The phase diagram of the resistor is as follows.

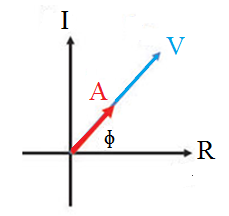
From the above phase diagram it’s clear that, in the case of a resistor, the voltage and the current are in phase.
The phase diagram of the inductor is as follows.

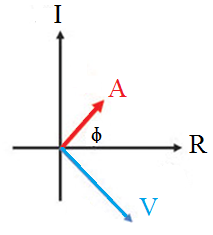
From the above phase diagram it’s clear that, in the case of an inductor, the voltage lags the current by a phase angle of ${}^{\pi }/{}_{2}$.

The phase diagram of the capacitor is as follows.

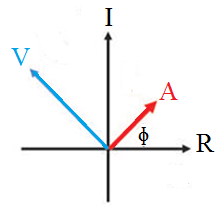
From the above phase diagram, it’s clear that, in the case of an inductor, the voltage leads the current by a phase angle of ${}^{\pi }/{}_{2}$.

Considering all the three-phase diagrams of the resistor, inductor and the capacitor, we have the results as follows.
The current in the case of the resistor, inductor and the capacitor are all in the phase with each other.
The voltage in the case of the resistor and the inductor differ by a phase angle of ${}^{\pi }/{}_{2}$. The voltage in the case of the resistor and the capacitor differ by a phase angle of ${}^{\pi }/{}_{2}$. The voltage in the case of the inductor and the capacitor differ by a phase angle of $\pi$.

As all the given statements are true, thus, the option (D) is correct.

Note:
The things to be on your finger-tips for further information on solving these types of problems are: The phase difference of the current in the case of resistor, inductor and capacitor is different from the phase difference of the voltage in the case of resistor, inductor and capacitor.