Solveeit Logo
Login

Question

Question: For a reaction consider the plot of \(\ln K\) versus \(1/T\) given in the figure. If the rate consta...

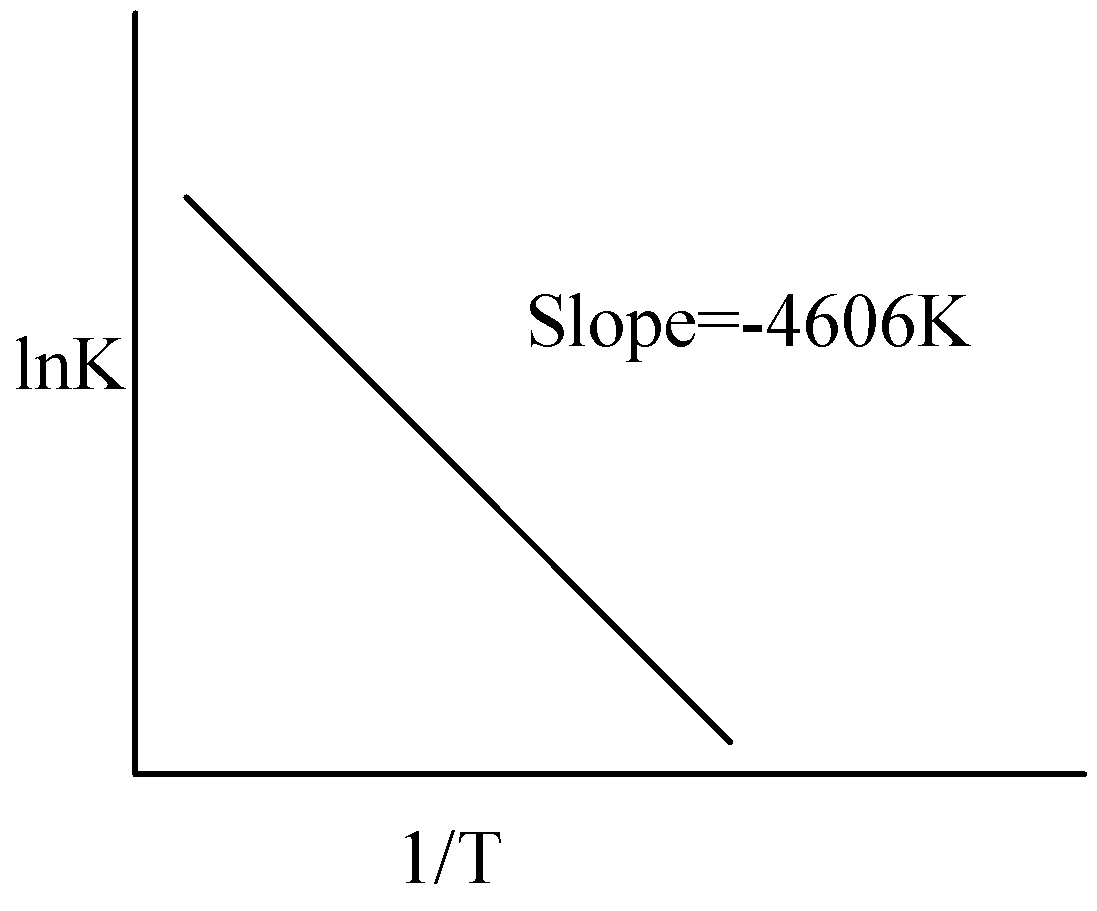
For a reaction consider the plot of ln⁡K\ln K versus 1/T1/T given in the figure. If the rate constant of this reaction at 400K400K is 10−5s−1{10^{ - 5}}{s^{ - 1}} , then the rate constant at 500K500K is:

A.2×10−4s−12 \times {10^{ - 4}}{s^{ - 1}}
B.10−4s−1{10^{ - 4}}{s^{ - 1}}
C.10−6s−1{10^{ - 6}}{s^{ - 1}}
D.4×10−4s−14 \times {10^{ - 4}}{s^{ - 1}}

Explanation

Solution

We have to know that the rate constant could be calculated using the Arrhenius equation. We have to derive the rate constant using the rate constant at 400K400K, both the temperatures and value of slope. The value of slope is −4606K - 4606K.

Complete step by step answer:
We have to know that the Arrhenius equation is useful in determining the rate of reaction and plays a significant portion in chemical kinetics. We could give Arrhenius equation as,
K=Ae−Ea/RTK = A{e^{ - {E_a}/RT}}
Here, K is the rate constant
A is the pre-exponential factor
Ea{E_a} is the activation energy
R is the gas constant
T is the temperature (in Kelvin)
The integrated form of Arrhenius equation is,
log⁡(K2K1)=Ea2.303R[1T2−1T1]\log \left( {\dfrac{{{K_2}}}{{{K_1}}}} \right) = \dfrac{{{E_a}}}{{2.303R}}\left[ {\dfrac{1}{{{T_2}}} - \dfrac{1}{{{T_1}}}} \right]
The value of temperature T1{T_1} is 400K400K .
The value of temperature T2{T_2} is 500K500K .
The rate constant at 400K400K is 10−5s−1{10^{ - 5}}{s^{ - 1}} .
We can write integrated equation as,
log⁡(K2K1)=Ea2.303R[1T2−1T1]\log \left( {\dfrac{{{K_2}}}{{{K_1}}}} \right) = \dfrac{{{E_a}}}{{2.303R}}\left[ {\dfrac{1}{{{T_2}}} - \dfrac{1}{{{T_1}}}} \right]
Let us substitute the known values in the above expression to calculate the rate constant.
We can calculate the rate constant as,
log⁡(K2K1)=Ea2.303R[1T2−1T1]\log \left( {\dfrac{{{K_2}}}{{{K_1}}}} \right) = \dfrac{{{E_a}}}{{2.303R}}\left[ {\dfrac{1}{{{T_2}}} - \dfrac{1}{{{T_1}}}} \right]
⇒2.303log⁡(K2K1)=EaR[1T1−1T2]\Rightarrow 2.303\log \left( {\dfrac{{{K_2}}}{{{K_1}}}} \right) = \dfrac{{{E_a}}}{R}\left[ {\dfrac{1}{{{T_1}}} - \dfrac{1}{{{T_2}}}} \right]
Now we can substitute the known values we get,
⇒2.303log⁡(K210−5)=4606[1400−1500]\Rightarrow 2.303\log \left( {\dfrac{{{K_2}}}{{{{10}^{ - 5}}}}} \right) = 4606\left[ {\dfrac{1}{{400}} - \dfrac{1}{{500}}} \right]
On simplifying we get,
K2=10−4s−1{K_2} = {10^{ - 4}}{s^{ - 1}}
The value of rate constant at 500K500K is 10−4s−1{10^{ - 4}}{s^{ - 1}}.
Therefore, the option (B) is correct.

Note:
We have to know that the fundamentals of the Arrhenius equation is collision theory. According to this theory, a reaction happens because of a collision between two molecules to form an intermediate. The formed intermediate is unstable and stays for a shorter period of time. The unstable intermediate gets broken into two product molecules and the energy used in formation of the intermediate is known as energy of activation. With the use of Arrhenius equation, we could determine the temperature, frequency, presence of catalyst, effect of energy wall and collision orientation.