Question

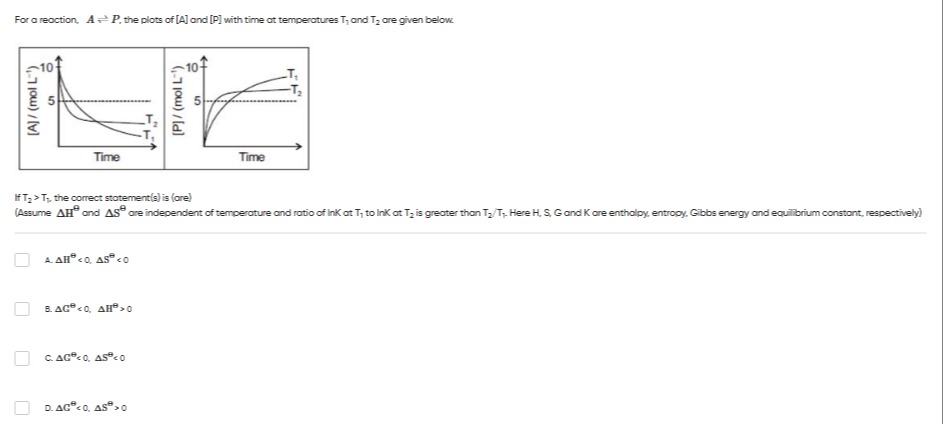
For a reaction, $A \rightleftharpoons P$, the plots of [A] and [P] with time at temperatures $T_1$ and $T_2$ are given below.

If $T_2 > T_1$, the correct statement(s) is (are) (Assume $\Delta H^\ominus$ and $\Delta S^\ominus$ are independent of temperature and ratio of $lnK$ at $T_1$ to $lnK$ at $T_2$ is greater than $T_2/T_1$. Here H, S, G and K are enthalpy, entropy, Gibbs energy and equilibrium constant, respectively)

• A. $\Delta H^\ominus < 0$, $\Delta S^\ominus < 0$
• B. $\Delta G^\ominus < 0$, $\Delta H^\ominus > 0$
• C. $\Delta G^\ominus < 0$, $\Delta S^\ominus < 0$
• D. $\Delta G^\ominus < 0$, $\Delta S^\ominus > 0$

Answer 1

Answer: (D)

$\Delta G^\ominus < 0$, $\Delta S^\ominus > 0$

Answer 2

At $T_1$, $[A]_{eq} > [P]_{eq}$, so $K_1 < 1$. At $T_2$, $[A]_{eq} < [P]_{eq}$, so $K_2 > 1$. Since $T_2 > T_1$ and $K$ increases with temperature, the forward reaction is endothermic ($\Delta H^\ominus > 0$). Since $K_2 > 1$, the reaction is spontaneous at $T_2$, so $\Delta G^\ominus(T_2) < 0$. Using $\Delta G^\ominus = \Delta H^\ominus - T \Delta S^\ominus$, we have $\Delta G^\ominus < 0$ and $\Delta H^\ominus > 0$. Thus, $\Delta H^\ominus - T \Delta S^\ominus < 0$, which implies $\Delta H^\ominus < T \Delta S^\ominus$. Since $\Delta H^\ominus > 0$, for this to hold, $\Delta S^\ominus$ must be positive ($\Delta S^\ominus > 0$). Therefore, $\Delta G^\ominus < 0$ and $\Delta S^\ominus > 0$.