Question

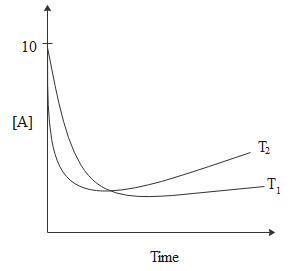
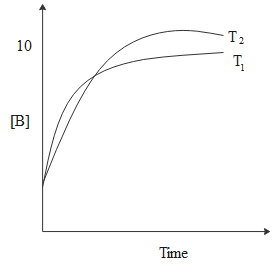
For a reaction, $A \rightleftharpoons P$, the plots of $\left[ A \right]$ and $\left[ P \right]$ with time at temperature ${T_1}$ and ${T_2}$ are given below. If ${T_2} > {T_1}$, the correct statement(s) is/are:
(Assume $\Delta {H^\theta }$ and $\Delta {S^\theta }$ are independent of temperature and ratio of $\ln K$ at ${T_1}$ and $\ln K$ at ${T_2}$ is greater than $\dfrac{{{T_2}}}{{{T_1}}}$. Here, $H,S,G$ and $K$ are enthalpy, entropy, Gibbs energy and equilibrium constant, respectively.)

A.$\Delta {H^\theta } < 0,\Delta {S^\theta } < 0$
B.$\Delta {H^\theta } > 0,\Delta {G^\theta } < 0$
C.$\Delta {S^\theta } < 0,\Delta {G^\theta } < 0$
D.$\Delta {S^\theta } > 0,\Delta {G^\theta } < 0$

Answer 1

To solve this question, you must recall the relation between the Gibbs free energy and equilibrium constant of a reaction. Gibbs free energy is a thermodynamic potential that is used to calculate the maximum work that can be performed by a system at a constant pressure and temperature.
Formula used:
$\Delta {G^\theta } = - RT\ln {K_{eq}}$
Where, $\Delta {G^\theta }$ is the change in free energy of reaction, ${K_{eq}}$ is the equilibrium constant of the reaction, $R$ is the gas constant and $T$ is the temperature.

Complete step by step answer:
In the given reaction,$A \rightleftharpoons P$
From the graph, we can see that at equilibrium $\left[ A \right] < 5$ and $\left[ P \right] > 5$.
Thus, we can write the equilibrium constant as, ${K_{eq}} = \dfrac{{\left[ A \right]}}{{\left[ P \right]}} > 1$.
Since $\Delta {G^\theta } = - RT\ln {K_{eq}}$, we can say that,$\Delta {G^\theta } < 0$.
We are given in the question that ${T_2} > {T_1}$.
From this we can infer, that,$\dfrac{{\ln {K_{{T_1}}}}}{{\ln {K_{{T_2}}}}} > \dfrac{{{T_2}}}{{{T_1}}} > 1$
$\Rightarrow \dfrac{{{K_{{T_1}}}}}{{{K_{{T_2}}}}} > 1 \\\ \Rightarrow {K_{{T_2}}} < {K_{{T_1}}} \\\$
This implies that the given reaction is exothermic which means that the change in enthalpy of the reaction will be zero.
$\Delta {H^\theta } < 0$
Also, we know that,
$\Delta {G^\theta } = \Delta {H^\theta } - T\Delta {S^\theta } \\\ \Rightarrow \Delta {S^\theta } = \dfrac{{\Delta {H^\theta } - \Delta {G^\theta }}}{T} \\\$
Since $\Delta {H^\theta } < 0$ and $\Delta {G^\theta } < 0$, it is necessary for the change in entropy to be negative; $\Delta {S^\theta } < 0$.
Therefore, the correct options are A and C.

Note:
The importance of the Gibbs function is that it is the single master variable that can determine whether a certain chemical change is thermodynamically possible. If the free energy of the reactants is greater than that of the products the reaction takes place spontaneously. $\Delta {G^\theta }$ is a key quantity in determining whether a reaction will take place in a given direction or not. For most reactions taking place in solutions or gaseous mixtures, the value of $\Delta {G^\theta }$ depends on the proportions of the various reaction components in the mixture; it is not a simple sum of the "products minus reactants" type, as is the case with $\Delta {H^\theta }$.