Question
Question: for a reaction, \[A\rightleftharpoons P\], the plots of \(\left[ A \right]\) and \(\left[ P \right]\...
for a reaction, A⇌P, the plots of [A] and [P] with time at temperature T1 and T2 are given below.
If T2>T1 , the correct state is/are:
(Assume ΔH∘ and ΔS∘ are independent of temperature and ratio of lnK at T1 to lnKat T2is greater than T1T2 . Here H,S,G and K are enthalpy, entropy, Gibbs energy and equilibrium constant, respectively.)
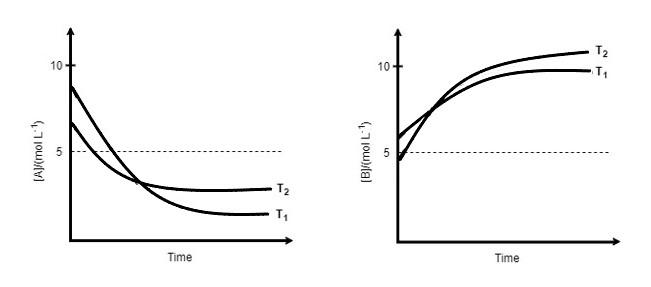
A. ΔH∘<0,ΔS∘<0
B. ΔG∘<0,ΔH∘>0
C. ΔG∘<0,ΔS∘<0
D. ΔG∘<0,ΔS∘>0
Solution
equilibrium is defined as the state of a system where the concentration of the reactant and the concentration of the product do not change with time and there will be no change in the properties of the system. A chemical equilibrium is achieved when the rate of forward reaction is equal to rate of backward reaction.
Complete step by step answer:
Enthalpy is defined as the sum of internal energy and the product of pressure and volume. The symbol of enthalpy is E. Enthalpy is the measurement of energy. When a process begins, the evolved heat becomes equal to the change in enthalpy at constant pressure. To calculate enthalpy change, we can write a mathematical expression as:
ΔH=ΔU+PΔV
Where ΔH is the change in enthalpy, ΔU is the change in internal energy, P is the pressure and ΔV is the change in volume.
Entropy is defined as the measure of thermal energy per unit temperature. The symbol of entropy is S. The SI unit of entropy is joules per Kelvin.
We can calculate entropy by:
ΔS=Tqrev
Where, ΔS Is change in entropy, qrev is the reverse of heat, T is the temperature.
According to the Arrhenius equation,
lnK=RT−Ea+lnA
Where, K is rate constants, Ea is activation energy, R is gas constant, T is temperature, A is pre exponential factor.
Here, as we can see that KαT1
Hence, lnK2lnK1>T1T2
As, T2>T1
On cross multiplying we get,
T1lnK1>T2lnK2
RT1lnK1>RTlnK2
As we know,
ΔG∘=−RTlnK
Therefore, ΔG∘<0
Hence, we can write it as,
(−ΔH∘+T1ΔS∘)>(−ΔH∘+T2ΔS∘)
ΔH∘<0
Therefore, T1ΔS∘>T2ΔS∘
T2>T1
Hence,
ΔS∘<0
So, the correct answer is Option A.
Note: Gibbs free energy is defined as the amount of work done when temperature and pressure remains constant in a thermodynamic system. The Arrhenius equation is used to tell the rate constant for an elementary step of reaction, it does not tell us about the rate of the reaction.
