Solveeit Logo
Login

Question

Question: For a ray of light refracting from medium \(1\) to medium \(2\) with plane interface, if unit vector...

For a ray of light refracting from medium 11 to medium 22 with plane interface, if unit vectors in the direction of incident ray, normal and the refracted ray are represented by {\overset{\lower0.5em\hbox{\smash{\scriptscriptstyle\frown}}}{k} _1},\overset{\lower0.5em\hbox{\smash{\scriptscriptstyle\frown}}}{n} and{\overset{\lower0.5em\hbox{\smash{\scriptscriptstyle\frown}}}{k} _2}respectively, and the angles of incidence and refraction byθ1{\theta _1}and θ2{\theta _2}respectively, then the Snell’s law for refraction at the interface can be written in vector form as

A.{\mu _2}{\overset{\lower0.5em\hbox{\smash{\scriptscriptstyle\frown}}}{k} _2} - {\mu _1}{\overset{\lower0.5em\hbox{\smash{\scriptscriptstyle\frown}}}{k} _1} = \left( {{\mu _1}\cos {\theta _1} - {\mu _2}\cos {\theta _2}} \right)\overset{\lower0.5em\hbox{\smash{\scriptscriptstyle\frown}}}{n}
B.{\mu _2}{\overset{\lower0.5em\hbox{\smash{\scriptscriptstyle\frown}}}{k} _2} - {\mu _1}{\overset{\lower0.5em\hbox{\smash{\scriptscriptstyle\frown}}}{k} _1} = \left( {{\mu _2}\sin {\theta _2} - {\mu _1}\sin {\theta _1}} \right)\overset{\lower0.5em\hbox{\smash{\scriptscriptstyle\frown}}}{n}
C.{\mu _1}{\overset{\lower0.5em\hbox{\smash{\scriptscriptstyle\frown}}}{k} _2} - {\mu _2}{\overset{\lower0.5em\hbox{\smash{\scriptscriptstyle\frown}}}{k} _1} = \left( {{\mu _2}\cos {\theta _2} - {\mu _1}\cos {\theta _1}} \right)\overset{\lower0.5em\hbox{\smash{\scriptscriptstyle\frown}}}{n}
D.{\mu _1}{\overset{\lower0.5em\hbox{\smash{\scriptscriptstyle\frown}}}{k} _1} - {\mu _2}{\overset{\lower0.5em\hbox{\smash{\scriptscriptstyle\frown}}}{k} _2} = \left( {{\mu _2}\sin {\theta _2} - {\mu _1}\sin {\theta _1}} \right)\overset{\lower0.5em\hbox{\smash{\scriptscriptstyle\frown}}}{n}

Explanation

Solution

To answer this question, we first need to write the Snell’s law for refraction in the form of a vector cross product. Then, manipulating the expression with the help of the vector triple product, we will get the final result.
Formula Used:
μ1sin⁡θ1=μ2sin⁡θ2{\mu _1}\sin {\theta _1} = {\mu _2}\sin {\theta _2}, here μ1{\mu _1}andμ2{\mu _2}are the refractive indices of the medium11 and the medium22respectively, and θ1{\theta _1}and θ2{\theta _2}are the angles made by the ray of light with the normal in the respective mediums.

Complete answer:
The situation is shown in the figure below.

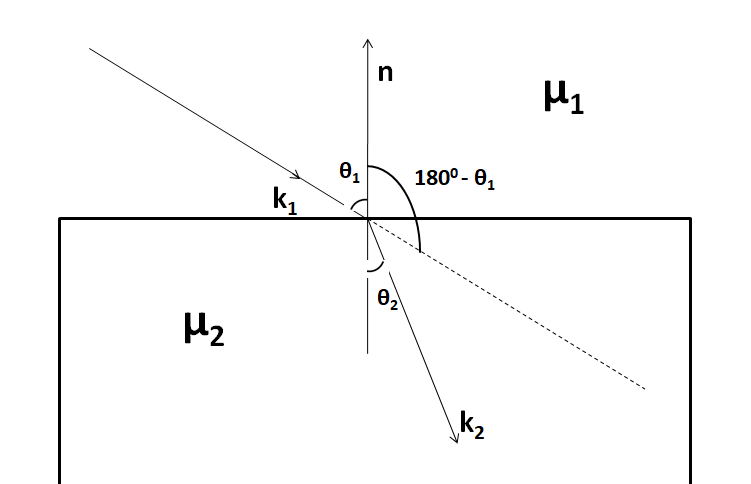
Applying Snell’s law at the interface, we have
μ1sin⁡θ1=μ2sin⁡θ2{\mu _1}\sin {\theta _1} = {\mu _2}\sin {\theta _2}
We know from trigonometry, that sin⁡θ=sin⁡(180∘−θ)\sin \theta = \sin \left( {{{180}^ \circ } - \theta } \right)
So, the Snell’s law can also be written as
μ1sin⁡(180∘−θ1)=μ2sin⁡(180∘−θ2){\mu _1}\sin \left( {{{180}^ \circ } - {\theta _1}} \right) = {\mu _2}\sin \left( {{{180}^ \circ } - {\theta _2}} \right) (1)
Now, we can see from the above figure that the angle between the unit vectors {\overset{\lower0.5em\hbox{\smash{\scriptscriptstyle\frown}}}{k} _1}and \overset{\lower0.5em\hbox{\smash{\scriptscriptstyle\frown}}}{n} is equal to180∘−θ1{180^ \circ } - {\theta _1}
So, we have k\lower0.5em⌢1×n\lower0.5em⌢=1×1×sin⁡(180∘−θ1)c\lower0.5em⌢{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{k} _1} \times \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{n} = 1 \times 1 \times \sin \left( {{{180}^ \circ } - {\theta _1}} \right)\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{c}
k\lower0.5em⌢1×n\lower0.5em⌢=sin⁡(180∘−θ1)c\lower0.5em⌢{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{k} _1} \times \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{n} = \sin \left( {{{180}^ \circ } - {\theta _1}} \right)\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{c} (2)
Similarly, we have
k\lower0.5em⌢2×n\lower0.5em⌢=sin⁡(180∘−θ2)c\lower0.5em⌢{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{k} _2} \times \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{n} = \sin \left( {{{180}^ \circ } - {\theta _2}} \right)\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{c} (3)
Here c\lower0.5em⌢\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{c} is the unit vector perpendicular to the plane of the paper.
Substituting (2) and (3) in (1), we get
μ1(k\lower0.5em⌢1×n\lower0.5em⌢)=μ2(k\lower0.5em⌢2×n\lower0.5em⌢){\mu _1}\left( {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{k} }_1} \times \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{n} } \right) = {\mu _2}\left( {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{k} }_2} \times \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{n} } \right)
Now, we take the cross product of the unit vector \overset{\lower0.5em\hbox{\smash{\scriptscriptstyle\frown}}}{n} with both the sides
μ1(n\lower0.5em⌢×(k\lower0.5em⌢1×n\lower0.5em⌢))=μ2(n\lower0.5em⌢×(k\lower0.5em⌢2×n\lower0.5em⌢)){\mu _1}\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{n} \times \left( {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{k} }_1} \times \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{n} } \right)} \right) = {\mu _2}\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{n} \times \left( {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{k} }_2} \times \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{n} } \right)} \right)
Writing the values of the vector triple products on both sides
μ1((n\lower0.5em⌢⋅n\lower0.5em⌢)k\lower0.5em⌢1−(n\lower0.5em⌢⋅k\lower0.5em⌢1)n\lower0.5em⌢)=μ2((n\lower0.5em⌢⋅n\lower0.5em⌢)k\lower0.5em⌢2−(n\lower0.5em⌢⋅k\lower0.5em⌢2)n\lower0.5em⌢){\mu _1}\left( {\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{n} \cdot \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{n} } \right){{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{k} }_1} - \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{n} \cdot {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{k} }_1}} \right)\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{n} } \right) = {\mu _2}\left( {\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{n} \cdot \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{n} } \right){{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{k} }_2} - \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{n} \cdot {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{k} }_2}} \right)\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{n} } \right) (4)
We have n\lower0.5em⌢⋅n\lower0.5em⌢=1×1=1\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{n} \cdot \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{n} = 1 \times 1 = 1
Also,
n\lower0.5em⌢⋅k\lower0.5em⌢1=1×1×cos⁡(180∘−θ1)\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{n} \cdot {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{k} _1} = 1 \times 1 \times \cos \left( {{{180}^ \circ } - {\theta _1}} \right)
n\lower0.5em⌢⋅k\lower0.5em⌢1=−cos⁡θ1\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{n} \cdot {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{k} _1} = - \cos {\theta _1}
Similarly
n\lower0.5em⌢⋅k\lower0.5em⌢2=−cos⁡θ2\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{n} \cdot {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{k} _2} = - \cos {\theta _2}
Putting these values in (4), we get
μ1(k\lower0.5em⌢1−(−cos⁡θ1)n\lower0.5em⌢)=μ2(k\lower0.5em⌢2−(−cos⁡θ2)n\lower0.5em⌢){\mu _1}\left( {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{k} }_1} - \left( { - \cos {\theta _1}} \right)\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{n} } \right) = {\mu _2}\left( {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{k} }_2} - \left( { - \cos {\theta _2}} \right)\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{n} } \right)
μ1(k\lower0.5em⌢1+(cos⁡θ1)n\lower0.5em⌢)=μ2(k\lower0.5em⌢2+(cos⁡θ2)n\lower0.5em⌢){\mu _1}\left( {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{k} }_1} + \left( {\cos {\theta _1}} \right)\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{n} } \right) = {\mu _2}\left( {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{k} }_2} + \left( {\cos {\theta _2}} \right)\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{n} } \right)
On multiplying, we get
μ1k\lower0.5em⌢1+μ1(cos⁡θ1)n\lower0.5em⌢=μ2k\lower0.5em⌢2+μ2(cos⁡θ2)n\lower0.5em⌢{\mu _1}{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{k} _1} + {\mu _1}\left( {\cos {\theta _1}} \right)\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{n} = {\mu _2}{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{k} _2} + {\mu _2}\left( {\cos {\theta _2}} \right)\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{n}
On rearranging the terms, we get
μ1cos⁡θ1n\lower0.5em⌢−μ2cos⁡θ2n\lower0.5em⌢=μ2k\lower0.5em⌢2−μ1k\lower0.5em⌢1{\mu _1}\cos {\theta _1}\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{n} - {\mu _2}\cos {\theta _2}\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{n} = {\mu _2}{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{k} _2} - {\mu _1}{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{k} _1}
Taking \overset{\lower0.5em\hbox{\smash{\scriptscriptstyle\frown}}}{n} as common, we finally get
μ2k\lower0.5em⌢2−μ1k\lower0.5em⌢1=(μ1cos⁡θ1−μ2cos⁡θ2)n\lower0.5em⌢{\mu _2}{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{k} _2} - {\mu _1}{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{k} _1} = \left( {{\mu _1}\cos {\theta _1} - {\mu _2}\cos {\theta _2}} \right)\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{n}

Hence, the correct answer is option A.

Note:
We used the vector triple product in this question just to manipulate our answer in the same form as the options were given. The idea is simple, as the vector triple product involves subtraction of the vectors, the form in which the options are given, so we used this method.