Question

For a quasi-static process $P - V$ curve is given as shown during the process as the state changes from $1$ to $2$, the work done by the system on surroundings is \\_\\_\\_\\_\\_ with respect to time.

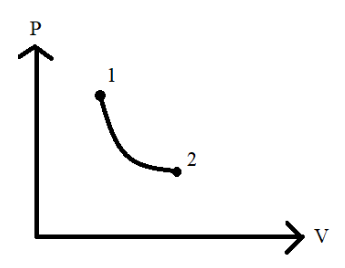
A. Constant
B. Continuously decreasing
C. Continuously increasing
D. First increases and then decreases

Answer 1

Thermodynamics is a branch of physics which signifies the concepts of heat and temperature and the conversions of heat to other forms of energy. The interpretation of the area under the $P - V$ graph is required in order to determine the solution to the problem. The relation between the work done and the $P - V$ curve is obtained in order to find the work done by the system on the surroundings.

Complete answer:
The above problem revolves around the concept of $P - V$ graph and its relationship with the work done by the system. In order to find this work done we first need to know the principle behind the $P - V$ curve and what a quasi-static process is.

The terms system and surrounding that we are referring to as given in the question must first be understood. System is defined as the large amount of particles having a certain value of pressure, volume and temperature while the surroundings are defined as everything apart from the system or in other words everything that is present outside the system which can have a direct effect on the system.

As we can see from the graph there is some effect of the surroundings on the system which leads to the change in state shown from point $1$ to $2$ in the graph. The changes occur in its pressure and volume and hence the above $P - V$ graph is given. Since there is a change in the system conditions there is said to be some amount of work done by the surroundings on the system to result in this change. We are asked to get this work done.

A quasi-static process refers to an infinitely slow process where the system remains in thermal and chemical equilibrium with its surroundings. This means that the temperature and pressure vary only by a small amount, that is, only infinitesimally from the conditions of the surroundings at every stage throughout the process. Hence, the process indicated in the graph above is extremely slow and the change in its state from $1$ to $2$ takes a long time.

We will now look into the interpretation of the $P - V$ graph that is given. The significance of a $P - V$ diagram is that the area under the $P - V$ graph specifies the work done on the system. The question mentions that a change in state occurs from $1$ to $2$. Thus the graph will be as shown below:

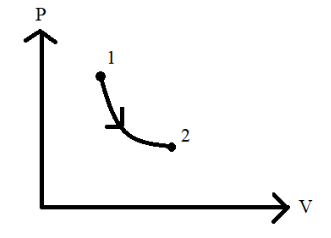
Thus, this means that the system in this case is undergoing expansion. Hence, when work is done, the system is said to undergo some expansion changing its pressure and volume conditions indicated by the $P - V$ graph diagram which is given. Let us take a look at the graph and the area under it at a certain time interval. The below diagram illustrates the area under the graph from point $1$ to $2$.

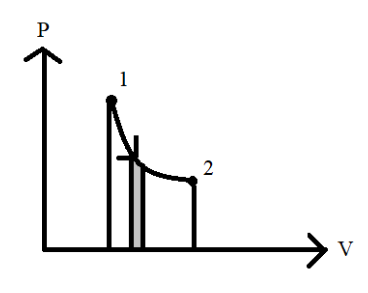
The strip of the area grey is considered as part of the area as shown in the above diagram.This area signifies a small part of the work done on the system since the area under the $P - V$ graph is equivalent to the work done on the system. The total work done for the entire process will be determined by adding by all the number of area strips under the $P - V$ graph. Thus, the work done in expanding the gas will be increased from $1$ to $2$.Hence the work done continuously by the system on surroundings increases with respect to time.

Therefore, the correct answer is option C.

Note: A common misconception that may occur will be that heat and work may be regarded as the same which is actually incorrect. Although they seem similar to each other they are different. Heat is said to be the equivalent to the energy transfer due to a change in temperature but the work done refers to the energy transfer brought about by factors which need not be temperature. A point to note here, is that thermodynamic processes in real life are generally not quasi-static in nature.