Question

For a point $P$ in the plane, let ${d_1}\left( P \right)$ and ${d_2}\left( P \right)$ be the distance of the point $P$ from the lines $x - y = 0$ and $x + y = 0$ respectively. The area of the region R consisting of all the points $P$ lying in the first quadrant of the plane and satisfying $2 \leqslant {d_1}\left( P \right) + {d_2}\left( P \right) \leqslant 4$ is
A. 4
B. 6
C. 10
D. 16

Answer 1

Two Dimensional Standard equation of the straight line:
$Ax + By + C = 0$
The distance between a point $A\left( {{x_0},{y_0}} \right)$ is given by the formula:
$d = \left| {\dfrac{{A{x_0} + B{y_0} + C}}{{\sqrt {{A^2} + {B^2}} }}} \right|$
It is stated that ${d_1}\left( P \right)$ and ${d_2}\left( P \right)$ are the distances of a point P from a straight line, use the distance formula between point and straight line to calculate their values.
Solve the given inequality and try to draw its graph.
Calculating areas from the graph is easy sometimes. Remember that the coordinate axes, y-axis, and x-axis are mutually perpendicular, therefore the line drawn vertical on these axes fall at ${90^ \circ }$
The solution region is the common area satisfying all inequality equations.

Complete step-by-step answer:
Draw the graphs of $x - y = 0$ and $x + y = 0$.

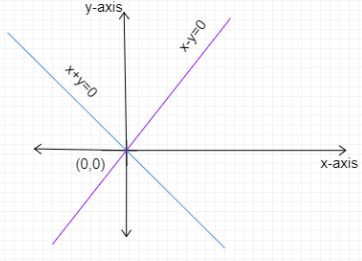
Given that ${d_1}\left( P \right)$ is the distance of the point $P$ from the lines $x - y = 0$
Let $\left( {{x_0},{y_0}} \right)$ is coordinated of point $P$
On comparing $x - y = 0$ with the standard equation of the line $Ax + By + C = 0$
$A = 1; \\\ B = - 1; \\\ C = 0. \\\$
Distance between a point $P\left( {{x_0},{y_0}} \right)$ from the line $x - y = 0$ is:
$d = \left| {\dfrac{{A{x_0} + B{y_0} + C}}{{\sqrt {{A^2} + {B^2}} }}} \right|$
$\Rightarrow \left| {\dfrac{{{x_0} + \left( { - 1} \right){y_0} + 0}}{{\sqrt {{1^2} + {{\left( { - 1} \right)}^2}} }}} \right|$
$\Rightarrow \left| {\dfrac{{{x_0} - {y_0}}}{{\sqrt 2 }}} \right|$
Thus, ${d_1}\left( P \right) = \left| {\dfrac{{{x_0} - {y_0}}}{{\sqrt 2 }}} \right|$
Given that ${d_2}\left( P \right)$ is the distance of the point $P$ from the lines $x + y = 0$
On comparing $x + y = 0$ with the standard equation of the line $Ax + By + C = 0$
$A = 1; \\\ B = 1; \\\ C = 0. \\\$
The distance between a point $P\left( {{x_0},{y_0}} \right)$ from the line $x + y = 0$ is:
$d = \left| {\dfrac{{A{x_0} + B{y_0} + C}}{{\sqrt {{A^2} + {B^2}} }}} \right|$
$\Rightarrow \left| {\dfrac{{{x_0} + {y_0} + 0}}{{\sqrt {{1^2} + {1^2}} }}} \right|$
$\Rightarrow \left| {\dfrac{{{x_0} + {y_0}}}{{\sqrt 2 }}} \right|$
Thus, ${d_2}\left( P \right) = \left| {\dfrac{{{x_0} + {y_0}}}{{\sqrt 2 }}} \right|$
$\Rightarrow {d_1}\left( P \right) + {d_2}\left( P \right)$ $= \left| {\dfrac{{{x_0} - {y_0}}}{{\sqrt 2 }}} \right| + \left| {\dfrac{{{x_0} + {y_0}}}{{\sqrt 2 }}} \right|$
Solve the given inequality:
$2 \leqslant {d_1}\left( P \right) + {d_2}\left( P \right) \leqslant 4$
$2 \leqslant \left| {\dfrac{{{x_0} - {y_0}}}{{\sqrt 2 }}} \right| + \left| {\dfrac{{{x_0} + {y_0}}}{{\sqrt 2 }}} \right| \leqslant 4$
$2\sqrt 2 \leqslant \left( {\left| {{x_0} - {y_0}} \right| + \left| {{x_0} + {y_0}} \right|} \right) \leqslant 4\sqrt 2$
Let $\left( {{x_0} > {y_0}} \right)$

$$\Rightarrow 2\sqrt 2 \leqslant \left( {{x_0} + {x_0}} \right) \leqslant 4\sqrt 2 \\\ \Rightarrow 2\sqrt 2 \leqslant \left( {2{x_0}} \right) \leqslant 4\sqrt 2 \\\$$

$\Rightarrow \sqrt 2 \leqslant {x_0} \leqslant 2\sqrt 2$
Let $\left( {{x_0} < {y_0}} \right)$

$$\Rightarrow 2\sqrt 2 \leqslant \left( {{y_0} + {y_0}} \right) \leqslant 4\sqrt 2 \\\ \Rightarrow 2\sqrt 2 \leqslant \left( {2{y_0}} \right) \leqslant 4\sqrt 2 \\\$$

$\Rightarrow \sqrt 2 \leqslant {y_0} \leqslant 2\sqrt 2$
Draw the graph of inequalities:
For inequality $\sqrt 2 \leqslant {x_0}$
Let ${x_0} = \sqrt 2$
Draw the vertical line at ${x_0} = \sqrt 2$
The feasible region (or solution region) of inequality $\sqrt 2 \leqslant {x_0}$ is the right side of the line ${x_0} = \sqrt 2$
For inequality ${x_0} \leqslant 2\sqrt 2$
Let ${x_0} = 2\sqrt 2$
Draw the vertical line at ${x_0} = 2\sqrt 2$
The feasible region (or solution region) of inequality ${x_0} \leqslant 2\sqrt 2$ is the left side of the line ${x_0} = 2\sqrt 2$
Thus the feasible region of the inequality $\sqrt 2 \leqslant {x_0} \leqslant 2\sqrt 2$ is the area between the vertical lines ${x_0} = \sqrt 2$ and ${x_0} = 2\sqrt 2$
For inequality $\sqrt 2 \leqslant {y_0}$
Let ${y_0} = \sqrt 2$
Draw the horizontal line at ${y_0} = \sqrt 2$
The feasible region (or solution region) of inequality $\sqrt 2 \leqslant {y_0}$ is upward of the line ${y_0} = \sqrt 2$
For inequality ${y_0} \leqslant 2\sqrt 2$
Let ${y_0} = 2\sqrt 2$
Draw the horizontal line at ${y_0} = 2\sqrt 2$
The feasible region (or solution region) of inequality ${y_0} \leqslant 2\sqrt 2$ is downward of the line ${y_0} = 2\sqrt 2$
Thus the feasible region of the inequality $\sqrt 2 \leqslant {y_0} \leqslant 2\sqrt 2$ is the area between the horizontal lines ${y_0} = \sqrt 2$ and ${y_0} = 2\sqrt 2$

The area of the region R consisting of all the points $P$ lying in the first quadrant of the plane
and satisfying $2 \leqslant {d_1}\left( P \right) + {d_2}\left( P \right) \leqslant 4$ i.e. $\sqrt 2 \leqslant {x_0} \leqslant 2\sqrt 2$ and $\sqrt 2 \leqslant {y_0} \leqslant 2\sqrt 2$
In other words, the common area between $\sqrt 2 \leqslant {x_0} \leqslant 2\sqrt 2$ and $\sqrt 2 \leqslant {y_0} \leqslant 2\sqrt 2$ ; and first quadrant.
Thus, in the following graph, the shaded portion is the required area.

Therefore, the coordinates from the graph are:
$A\left( {0,0} \right);{\text{ B}}\left( {\sqrt 2 ,0} \right){\text{; }}C\left( {2\sqrt 2 ,0} \right);{\text{ }}D\left( {2\sqrt 2 ,2\sqrt 2 } \right);{\text{ }}E\left( {0,2\sqrt 2 } \right);{\text{ }}F\left( {0,\sqrt 2 } \right);{\text{ }}G\left( {\sqrt 2 ,\sqrt 2 } \right)$
From the graph, Length $AC = 2\sqrt 2 {\text{ }}units,{\text{ }}CD = 2\sqrt 2 {\text{ }}units,{\text{ }}DE = 2\sqrt 2 {\text{ }}units,{\text{ }}AE = 2\sqrt 2 {\text{ }}units.$
Thus ACDE forms a square of side $= 2\sqrt 2 {\text{ }}units$.
Therefore, the area of square ACDE $= {\text{side} \times {side}}sq.units$
$\Rightarrow 2\sqrt 2 \times 2\sqrt 2 {\text{ }}sq.units \\\ \Rightarrow 8{\text{ }}sq.units \\\$
From the graph, Length $AB = \sqrt 2 {\text{ }}units,{\text{ BG}} = \sqrt 2 {\text{ }}units,{\text{ GF}} = \sqrt 2 {\text{ }}units,{\text{ }}AF = \sqrt 2 {\text{ }}units.$
Thus ABGF forms a square of side $= \sqrt 2 {\text{ }}units$.
Therefore, the area of square ABGF $= {\text{side} \times {side}}sq.units$
$\Rightarrow \sqrt 2 \times \sqrt 2 {\text{ }}sq.units \\\ \Rightarrow 2{\text{ }}sq.units \\\$
Area of shaded portion = area of square ACDE - area of square ABGF
$= 8 - 2{\text{ }}sq.units \\\ = 6{\text{ }}sq.units \\\$
The area of the region R consisting of all the points $P$ lying in the first quadrant of the plane and satisfying $2 \leqslant {d_1}\left( P \right) + {d_2}\left( P \right) \leqslant 4$is 6 sq. units.

So, the correct answer is “Option B”.

Note: Students should always remember the quantity “distance” can never be negative. So, the modulus is used in the formula.
$d = \left| {\dfrac{{A{x_0} + B{y_0} + C}}{{\sqrt {{A^2} + {B^2}} }}} \right|$
Students might go wrong while shading the solution region of an inequality region. Let’s understand the concept so that you guys won’t make mistakes.
An example is given: Draw the graph of $5x + y \leqslant 100$
Draw the graph of $5x + y = 100$

x	0	20
y	100	0

           ![](https://www.vedantu.com/question-sets/ade61a3d-8071-4dcb-b13a-350bcfbe67eb7251363672757894416.png)  

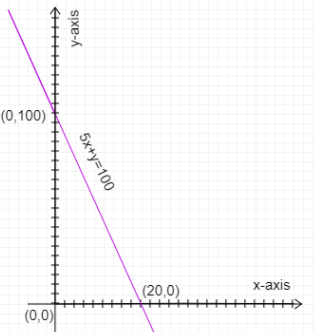
Graph: $5x + y = 100$
The line $5x + y = 100$ divides the XY plane into two parts, one it to the left side of the line and the other is the right side of the line.
Consider a point in the XY plane.
Let the point is the origin (0,0)
Check whether the considered point satisfies the inequality or not.
$5x + y \leqslant 100$
$\Rightarrow 5\left( 0 \right) + \left( 0 \right) \leqslant 100$
Yes. (0,0) satisfies the inequality $5x + y \leqslant 100$
The point (0,0) lies on the left side of the inequality $5x + y \leqslant 100$. Thus the feasible region is the left side of the inequality $5x + y \leqslant 100$.

           ![](https://www.vedantu.com/question-sets/fce83790-bd8e-4787-8ebf-9175dfbb37813383581776144956111.png)  

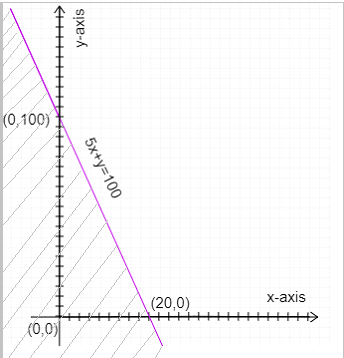
Graph: solution region
If the considered point does not satisfy the inequality then the side opposite to the point is the feasible region.