Question

For a particle performing uniform circular motion.
A. Magnitude of particle velocity (speed) remains constant.
B. Particle velocity remains directed perpendicular to the radius vector.
C. Direction of acceleration keeps changing as the particle moves.
D. Direction of acceleration does not remain constant.

Answer 1

Speed will be constant throughout. For a particle performing uniform circular motion. Speed will be constant throughout. Velocity will be tangential in the direction of motion at a particular point. Speed is constant, hence tangential acceleration is zero.

Complete step by step answer:
Let’s consider, as particles revolve around the circumference of a circle. The motion performed by particles is uniform circular motion.
So first let’s understand what uniform circular motion is. A uniform circular motion is the motion of a particle along the circumference of a circle with constant speed. It is also represented as U.C.M.
In uniform circular motion, the direction of velocity is along the tangent drawn to the position of the particle on the circumference of the circle. You can imagine this in the diagram given below. Hence the direction of velocity goes on changing continuously. However magnitude of velocity is constant i.e. Speed of particles is constant. Hence the magnitude of angular velocity is constant.
Examples of uniform circular motion are motion of earth around the sun, motion of moon around the moon.
As you can see in the diagram, the radius vector $\vec{r}$ is perpendicular to the particle velocity which we calculated by drawing tangent. So particle velocity will always be perpendicular to the radius vector. Radius vector is nothing but the radius of the circle having direction.
We know that acceleration is the time rate of change of velocity and velocity is the vector quantity, which requires both magnitude and direction for its completion and acceleration is a derivative of velocity. Hence the direction of acceleration keeps changing as the particle moves.

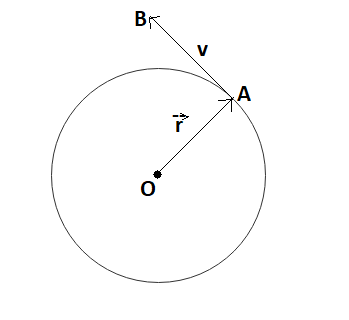
where OA is the radius of the circle,
and AB is the tangent drawn perpendicular to the radius

Hence, the correct answer is option A.

Note:
However, the magnitude of velocity is constant. Hence the magnitude of angular velocity is constant. Therefore it can also be defined as periodic motion of a particle moving along the circumference of a circle with constant angular speed. In U.C.M. speed, radial acceleration, kinetic energy, angular momentum, magnitude of linear momentum remain constant. Speed and velocity are two different things. Velocity is a vector quantity having magnitude and direction and speed is the scalar quantity. Speed is a magnitude of velocity. If one of them i.e. either magnitude of direction of velocity, will change then acceleration will also change.