Question

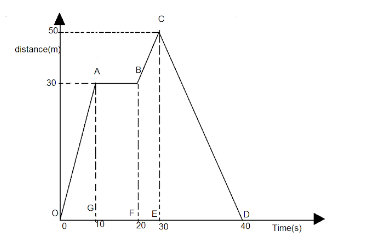
For a particle in motion, the distance- time graph is shown in the figure. From graph, answer the following:
(1) During which time period the particle is stationary.
(2) Find magnitude of the velocity in $OA$ , $AB$ and $BC$ parts.

Answer 1

Hint : In order to solve this question, we are going to first find the time period in which the particle is stationary i.e. where the displacement is zero. Then, we will find the magnitude of the velocities for each part by taking the distances and the time periods from the graph.
The velocity for the particle is calculated as:
$v = \dfrac{d}{t}$
Where $d$ is displacement and $t$ is time period.

Complete Step By Step Answer:
The given graph is a displacement- time graph, let us analyze all the time periods and figure out in which time period, the particle is stationary.
When the particle will be stationary, the displacement will remain constant while the time will keep on changing, as we can see that the time period between the points $A$ and $B$ , the displacement is constant, hence velocity is zero.
Thus, the time period between $A$ and $B$ is $\left( {20 - 10} \right)s = 10s$
Finding the velocity of the particle in parts $OA$ , $AB$ and $BC$ :
In the part $OA$ , we have, the displacement, $d = 30m$ and the time, $t = 10s$
Now finding the velocity for the particle, we get
$v = \dfrac{d}{t}$
Putting the values we get
$v = \dfrac{{30}}{{10}} = 3m{s^{ - 1}}$
In the part $AB$ , we have the displacement and time as ,
d = 0m \\\ t = 10s \\\
Then, the velocity can be calculated as:
$v = \dfrac{0}{{10}} = 0m{s^{ - 1}}$
Now for the third part $BC$ , the displacement is
$\left( {50 - 30} \right) = 20m$
And the time period is $t = 10s$
Hence, the velocity is
$v = \dfrac{{20}}{{10}} = 2m{s^{ - 1}}$
The magnitude of the velocity of particle in parts $OA$ , $AB$ and $BC$ :
$3m{s^{ - 1}},0m{s^{ - 1}},2m{s^{ - 1}}$

Note :
The slope of this displacement time graph gives the velocity of the particle while the slope is calculated either by taking the tangent of the curve or by dividing the change in the displacement with the time period. When there is no change in the displacement, the particle is stationary.