Question

For a particle in a uniformly accelerated circular motion
(A) Velocity is radial and acceleration has both radial and transverse components.
(B) Velocity is transverse and acceleration has both radial and transverse components.
(C) Velocity is radial and acceleration is transverse only.
(D) Velocity is transverse and acceleration is radial only.

Answer 1

In physics, circular motion is a movement of an object along the circumference of a circle or rotation along a circular path. It can be uniform, with constant angular rate of rotation and constant speed, or non uniform with a changing rate of rotation.
Uniform circular motion can be described as the motion of an object in a circle at a constant speed. As an object moves in a circle, it is constantly changing its direction. At all instances, the object is moving tangent to the circle. Since the direction of the velocity vector is the same as the direction of the object's motion, the velocity vector is directed tangent to the circle as well.

Complete step by step solution

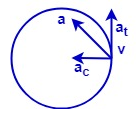
In case of uniformly accelerated circular motion, the velocity of the particle is always tangential / transverse.
But its acceleration has two components:
Radial component which acts towards the center of the motion.
Tangential / transverse component which is parallel to the direction of velocity.
Therefore, option (B) is the correct answer.

Note
The radial acceleration is due to the centripetal force exerted by the pull of the point around which the circular motion is taking place.
The tangential / transverse acceleration is due to the centrifugal force exerted on the body which is pushing the body out of its circular motion.
In a uniform circular motion this centrifugal and the centripetal forces are equal and opposite to each other to keep the body moving. In a uniform circular motion, the direction of the velocity changes constantly, so there is always an associated acceleration, even though the speed might be constant.