Question

For a particle executing simple harmonic motion, the displacement $x$ is given by $x = A\cos \omega t$. Identify the graph, which represents the variation of potential energy $\left( U \right)$ as a function of time $t$ and displacement $x$.

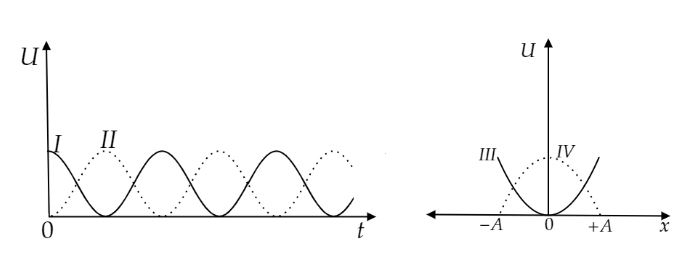
A. I, III
B. II, III
C. I, IV
D. II, IV

Answer 1

The potential energy of a body in simple harmonic motion (S.H.M.) is directly proportional the square of its displacement. The potential energy is equal to the work done by the restoring force acting on the particle in S.H.M.

Complete step by step answer:
For a particle in simple harmonic motion, the force acting the particle is $F = - kx$.
Where, $k$ is a force constant and $x$ is the distance of the particle from its equilibrium position. Let $dW$be work done by the force in displacing the particle through a small distance $dx$.
$dW = - Fdx$
$\Rightarrow dW = kxdx$
The total work done for the displacement $x$ is obtained by integrating the above equation between the limits $0$ to $x$.
$\int_0^W {dW} = \int_0^x {kxdx}$

On integration
$\Rightarrow \left[ W \right]_0^W = \left[ {\dfrac{{k{x^2}}}{2}} \right]_0^x$
Further calculating
$\Rightarrow W = \dfrac{1}{2}k{x^2}$
We know that the work done is equal to the potential energy of the particle.
Potential energy $U = \dfrac{1}{2}k{x^2}$
Again, $k = m{\omega ^2}$
Where, $m$ is the mass of the particle and $\omega$ is the angular speed of the particle.
Therefore, $U = \dfrac{1}{2}m{\omega ^2}{x^2}$ …… (1)
It is given that the displacement $x = A\cos \omega t$.
Substitute the value of $x$ in the above equation (1).
$U = \dfrac{1}{2}m{\omega ^2}{A^2}{\cos ^2}\omega t$ …… (2)

Now consider the equation (1).
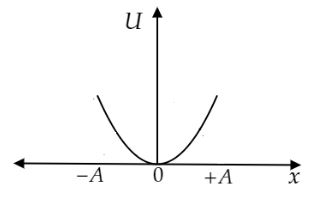
At $x = 0$, $U = 0$ i.e., potential energy is minimum.
At $x = \pm A$, $U = \dfrac{1}{2}m{\omega ^2}{A^2}$ i.e., potential energy is maximum.
So, the variation of potential energy $\left( U \right)$ with displacement $\left( x \right)$ is shown below.

Now consider the equation (2).
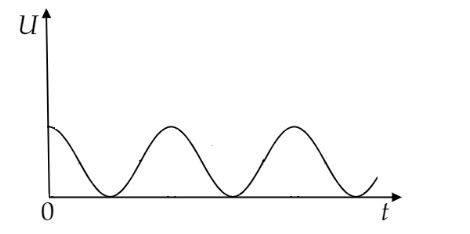
Potential energy $U$ is a function of ${\cos ^2}\omega t$.
At $t = 0$, ${\cos ^2}0 = 1$ i.e., potential energy will be maximum.
At $t = \dfrac{\pi }{{2\omega }}$, ${\cos ^2}\left( {\dfrac{\pi }{2}} \right) = 0$ i.e., potential energy will be minimum.
So, the variation of potential energy $\left( U \right)$ with time $\left( t \right)$ is shown below.

Hence, the correct option is A.

Note: Simple harmonic motion is the motion in which the restoring force is proportional to its displacement from the mean position and opposes its increase. The total energy of the particle in S.H.M. always remains constant. It is shown in the below additional information.