Question

For a parabola, it is given that the equation of the directrix is $x+y=4$ and coordinates of focus F (6, 6). Find:
(a) The tangent at vertex.
(b) And length of the latus rectum

Answer 1

First of all, we are going to find the equation of a parabola which we do by assuming a point say $\left( x,y \right)$ on the parabola then we know that the distance from this point to the focus and directrix are equal. After finding the equation of a parabola, we will find the tangent at vertex. For that we have to find the vertex of the parabola which is the intersection of the parabola with a line of symmetry. Then to find the equation of tangent, we need a slope so differentiate the equation of a parabola and substitute the value of x and y as the vertex of the parabola. Now, you will get the slope and the point so you can write the equation of a line. Now, the length of the latus rectum is 4 times the focal length.

Complete step-by-step answer:
We have given the equation of a directrix of parabola as:
$x+y=4$
And also coordinates of the focus are given as:
F (6, 6)
We are going to find the equation of a parabola as follows:
We know that distances from a point on the parabola to directrix and to the focus are equal. Now, let us suppose that point on the parabola is (x, y) so equating the distance from this point to the focus and the directrix we get,
We know that, distance formula between two points $\left( {{x}_{1}},{{y}_{1}} \right)\And \left( {{x}_{2}},{{y}_{2}} \right)$ is equal to:
$\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}$
So, using this distance formula we are going to find the distance from the point (x, y) to F (6, 6):
$\sqrt{{{\left( x-6 \right)}^{2}}+{{\left( y-6 \right)}^{2}}}$ ………. Eq. (1)
Now, we are going to find the distance between the point (x, y) and the directrix $x+y=4$ as follows:
$\begin{aligned} & \dfrac{\left| x+y-4 \right|}{\sqrt{1+1}} \\\ & =\dfrac{x+y-4}{\sqrt{2}}............Eq.(2) \\\ \end{aligned}$
Equating eq. (1) with eq. (2) we get,
$\sqrt{{{\left( x-6 \right)}^{2}}+{{\left( y-6 \right)}^{2}}}=\dfrac{x+y-4}{\sqrt{2}}$
Squaring both the sides we get,
$\begin{aligned} & {{\left( x-6 \right)}^{2}}+{{\left( y-6 \right)}^{2}}={{\left( \dfrac{x+y-4}{\sqrt{2}} \right)}^{2}} \\\ & \Rightarrow {{\left( x-6 \right)}^{2}}+{{\left( y-6 \right)}^{2}}=\dfrac{{{x}^{2}}+{{y}^{2}}+16+2xy-8y-8x}{2} \\\ & \Rightarrow 2\left( {{x}^{2}}-12x+36+{{y}^{2}}-12y+36 \right)={{x}^{2}}+{{y}^{2}}+16+2xy-8y-8x \\\ & \Rightarrow {{x}^{2}}+{{y}^{2}}-16x+128-16y-2xy=0 \\\ \end{aligned}$
In the above equation we can write ${{x}^{2}}-2xy+{{y}^{2}}={{\left( x-y \right)}^{2}}$ as follows:
$\begin{aligned} & \Rightarrow {{\left( x-y \right)}^{2}}-16\left( x+y \right)+128=0 \\\ & \Rightarrow {{\left( x-y \right)}^{2}}=16\left( x+y \right)-128 \\\ & \Rightarrow {{\left( x-y \right)}^{2}}=16\left( x+y-8 \right) \\\ \end{aligned}$
Hence, we got the equation of parabola as ${{\left( x-y \right)}^{2}}=16\left( x+y-8 \right)$.
Now, to find coordinates of vertex we will put the expressions written in the bracket as 0.
$\begin{aligned} & x-y=0........Eq.(1) \\\ & x+y-8=0.........Eq.(2) \\\ \end{aligned}$
From eq. (1) we get,
$x=y$
Now, substituting $x=y$ in eq. (2) we get,
$\begin{aligned} & y+y-8=0 \\\ & \Rightarrow 2y-8=0 \\\ & \Rightarrow 2y=8 \\\ & \Rightarrow y=4 \\\ \end{aligned}$
Now, $x=y$ so $x=y=4$.
Hence, we got the vertex of the parabola as $\left( 4,4 \right)$.
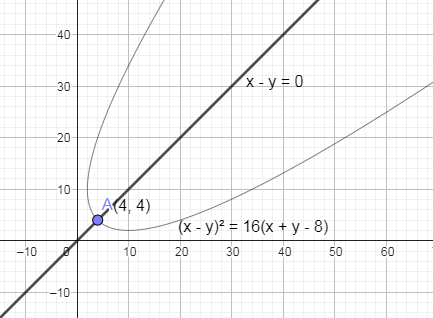
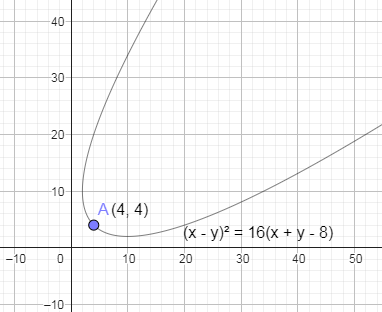
In the below figure, we have shown the parabola with vertex A (4, 4).

Now, in the first part (a), we have to find the tangent at the vertex of the parabola. For that, we are going to differentiate the equation of parabola on both the sides.
$\begin{aligned} & {{\left( x-y \right)}^{2}}=16\left( x+y-8 \right) \\\ & 2\left( x-y \right)\left( 1-\dfrac{dy}{dx} \right)=16\left( 1+\dfrac{dy}{dx} \right) \\\ \end{aligned}$
We have differentiated above by chain rule.
Now, clubbing the term which have $\dfrac{dy}{dx}$ on one side of the equation and remaining terms on the other side we get,
$\begin{aligned} & \dfrac{dy}{dx}\left( -2\left( x-y \right)-16 \right)=16-2\left( x-y \right) \\\ & \Rightarrow \dfrac{dy}{dx}=\dfrac{16-2\left( x-y \right)}{\left( -2\left( x-y \right)-16 \right)} \\\ \end{aligned}$
Taking negative sign as common from the numerator and denominator of the above equation we get,
$\dfrac{dy}{dx}=\dfrac{2\left( x-y \right)-16}{\left( 2\left( x-y \right)+16 \right)}$
Now, we have to find the slope at the vertex A (4, 4) of the parabola so substituting the values of x and y as $x=y=4$ in the above.
$\begin{aligned} & \dfrac{dy}{dx}=\dfrac{2\left( 4-4 \right)-16}{\left( 2\left( 4-4 \right)+16 \right)} \\\ & \Rightarrow \dfrac{dy}{dx}=\dfrac{-16}{16}=-1 \\\ \end{aligned}$
Hence, we get the slope of the tangent at the vertex A as -1. Now, we have slope of the tangent and also the point (4, 4) through which the tangent is passing so we can write the equation of tangent.
We know that, the equation of a line with slope “m” and the point $\left( {{x}_{1}},{{y}_{1}} \right)$ through which it passes through is:
$y-{{y}_{1}}=m\left( x-{{x}_{1}} \right)$
Using the above formula, in finding the equation of tangent we get,
$\begin{aligned} & y-4=\left( -1 \right)\left( x-4 \right) \\\ & \Rightarrow y-4=-x+4 \\\ & \Rightarrow x+y=8 \\\ \end{aligned}$
Hence, we got the equation of tangent at the vertex A (4, 4) as $x+y=8$.
Now, in the second part (b) of the above problem we have to find the length of the latus rectum.
As we know, the length of the latus rectum is 4 times the focal length of the parabola.
Focal length of the parabola of the equation ${{y}^{2}}=4ax$ is “a”. Now, focal length of the parabola of this problem is:
${{\left( x-y \right)}^{2}}=16\left( x+y-8 \right)$
Comparing the above parabola with ${{y}^{2}}=4ax$ we will find that:
$\begin{aligned} & 4a=16 \\\ & \Rightarrow a=4 \\\ \end{aligned}$
From the above, we get the focal length of the parabola as 4 so latus rectum is equal to:
$\begin{aligned} & 4\times 4 \\\ & =16 \\\ \end{aligned}$
Hence, we got the latus rectum as 16.

Note: The point to be noted that as you can see the equation of parabola that we are getting in this parabola is not the standard form of parabola like ${{y}^{2}}=4ax;{{x}^{2}}=4ay$ so while solving the equation of parabola, don’t think that you are going in the wrong direction. The point of difference of the parabola given in this problem with the standard parabolas is that in standard parabolas, the line of symmetries are x and y axis whereas the line of symmetry in the given parabola is $x-y=0$.
In the below diagram, we have shown the given parabola along with the line of symmetry as $x-y=0$.