Question

For a parabola; directrix: $x+y=4$and F: (6,6). Find
a) Endpoints of latus rectum
b) Equation of latus rectum

Answer 1

We know that the point on the parabola is equidistant from a fixed line and a fixed point. The fixed line is called the directrix of the parabola and the fixed point is called focus. The line joining the directrix and the point on parabola is perpendicular to the directrix. We will now calculate the distance between the point and directrix using formula $d=\left| \dfrac{A{{x}_{1}}+B{{y}_{1}}+C}{\sqrt{{{A}^{2}}+{{B}^{2}}}} \right|$ and the distance between the point and focus using formula$\begin{aligned} & d\text{=}\sqrt{{{\left( {{x}_{1}}-{{x}_{2}} \right)}^{2}}+{{\left( {{y}_{1}}-{{y}_{2}} \right)}^{^{2}}}} \\\ & \\\ \end{aligned}$ . We will now equate them as the point is Equidistant. We will get the equation of the Parabola. We also know that the Latus rectum of the parabola passes through the focus and is parallel to the directrix. We will calculate the equation of the Latus Rectum. We know that latus rectum and parabola intersect each other so the equation will satisfy each other. Hence, we can calculate the end point of the latus rectum.

Complete step-by-step answer:

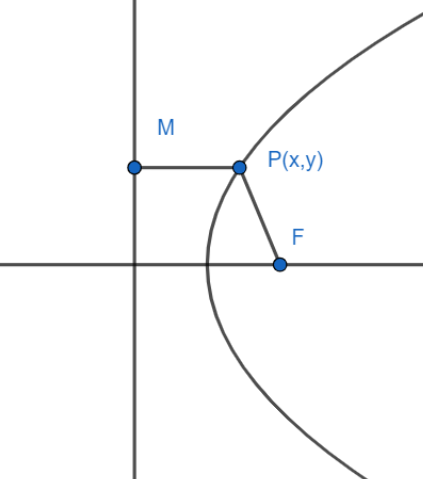
Let’s assume point P:(x, y) on parabola,
Let perpendicular line joining point P and directrix meet at point M
We know that, the point on the parabola is equidistant from a fixed line and a fixed point.
So, PM=PF
The equation of Directrix: $x+y=4$ can be written as
$\Rightarrow x+y-4=0$
We know the perpendicular distance between a line and a point is given by
$d=\left| \dfrac{A{{x}_{1}}+B{{y}_{1}}+C}{\sqrt{{{A}^{2}}+{{B}^{2}}}} \right|$
Distance between P and M is PM
$PM=\left| \dfrac{A{{x}_{1}}+B{{y}_{1}}+C}{\sqrt{{{A}^{2}}+{{B}^{2}}}} \right|$
Where A=1, B=1 and C=-4
And ${{x}_{1}}=x$ , ${{y}_{1}}=y$

& \Rightarrow \text{PM=}\left| \dfrac{1.x+1.y-4}{\sqrt{{{1}^{2}}+{{1}^{2}}}} \right| \\\ & \Rightarrow \text{PM=}\dfrac{x+y-4}{\sqrt{2}} \\\ \end{aligned}$$ The distance PF can be calculated using distance formula $$\Rightarrow d\text{=}\sqrt{{{\left( {{x}_{1}}-{{x}_{2}} \right)}^{2}}+{{\left( {{y}_{1}}-{{y}_{2}} \right)}^{^{2}}}}$$ Where $${{x}_{1}}\text{=}x$$ and $${{y}_{1}}=y$$ And $${{x}_{2}}=6$$, $${{y}_{2}}\text{=6}$$ $$\Rightarrow \text{PF=}\sqrt{{{\left( x-6 \right)}^{2}}+{{\left( y-6 \right)}^{^{2}}}}$$ Now PF=PM $$\sqrt{{{\left( x-6 \right)}^{2}}+{{\left( y-6 \right)}^{^{2}}}}=\dfrac{x+y-4}{\sqrt{2}}$$ We will now square on both the sides $$\text{P}{{\text{F}}^{2}}\text{=P}{{\text{M}}^{2}}$$ , we get, $$\begin{aligned} & \Rightarrow {{\left( x-6 \right)}^{2}}+{{\left( y-6 \right)}^{^{2}}}=\dfrac{{{(x+y-4)}^{2}}}{2} \\\ & \Rightarrow {{x}^{2}}+{{y}^{2}}-12\left( x+y \right)+72=\dfrac{{{x}^{2}}+{{y}^{2}}-8\left( x+y \right)+2xy+16}{2} \\\ & \Rightarrow 2{{x}^{2}}+2{{y}^{2}}-24\left( x+y \right)+144={{x}^{2}}+{{y}^{2}}-8\left( x+y \right)+2xy+16 \\\ & \Rightarrow {{x}^{2}}+{{y}^{2}}-16x-16y-2xy+128=0..........(i) \\\ \end{aligned}$$ Equation ($$i$$) gives the equation of the Parabola Now we know that the Directrix is parallel to the Latus rectum. Hence, their slope will be equal. The equation of the Latus Rectum can be written as $$\Rightarrow x+y+c=0$$ As the latus rectum passes through the focus F: (6,6). Therefore, it will satisfy the equation. We will put value of x and y in above equation, we will get the value of c $$\begin{aligned} & \Rightarrow 6+6+c=0 \\\ & \Rightarrow c=-12 \\\ \end{aligned}$$ Equation the latus rectum is $$\Rightarrow x+y-12=0$$ The above equation can be written as $$\begin{aligned} & \Rightarrow y=12-x \\\ & \Rightarrow y=-(x-12)........(ii) \\\ \end{aligned}$$ As we know that latus rectum intersects the parabola. So, equation (ii) will satisfy the equation of parabola. Putting value of y from (ii) in equation (i), we get $$\begin{aligned} & \Rightarrow {{x}^{2}}+{{(-(x-12))}^{2}}-16x+16(x-12)+2x(x-12)+128=0 \\\ & \Rightarrow {{x}^{2}}+{{(x-12)}^{2}}-16x+16x-16*12+2{{x}^{2}}-24x+128=0 \\\ & \Rightarrow {{x}^{2}}+{{x}^{2}}+144-24x-192+2{{x}^{2}}-24x+128=0 \\\ & \Rightarrow 4{{x}^{2}}-48x+80=0 \\\ & \Rightarrow {{x}^{2}}-12x+20=0 \\\ & \\\ \end{aligned}$$ We will solve the above equation to get the value of x $$\begin{aligned} & \Rightarrow {{x}^{2}}-10x-2x+20=0 \\\ & \Rightarrow x(x-10)-2(x-10)=0 \\\ & \Rightarrow (x-10)(x-2)=0 \\\ & \Rightarrow x=2,10 \\\ \end{aligned}$$ By putting the value of x in equation (ii) $$\begin{aligned} & \Rightarrow y=-(x-12) \\\ & \\\ & \Rightarrow \text{For }x=2\text{ ; }y=10 \\\ & \Rightarrow \text{For }x=10\text{ };\text{ }y=2 \\\ \end{aligned}$$ Therefore, the end points of the latus rectum are (2,10) and (10,2) **Note:** In solving problems on conic sections majority of the times concepts and formulae of Straight lines are used so you should have the idea of them. When the two lines are parallel to each other only their slopes are equal so don’t assume that equations are also equal.