Question

For a linear plot of $\log (x/m)$ versus $\log p$ in a Freundlich adsorption isotherm, which of the following statements is correct ? ($k$and $n$ are constants)
A. $\dfrac{1}{n}$ appears as the intercept.
B. Only $\dfrac{1}{n}$ appears as the slope.
C. log$\dfrac{1}{n}$ appears as the intercept.
D. Both $k$ and $\dfrac{1}{n}$ appear in the slope term

Answer 1

An adsorption isotherm is a curve relating the equilibrium concentration of a solute on the surface of an adsorbent. The adsorption isotherm is also an equation relating the amount of solute adsorbed onto the solid.

Complete step by step answer:
Freundlich Adsorption Isotherm gives the variation in the quantity of gas adsorbed by a unit mass of solid adsorbent with the change in pressure of the system for a given temperature. The expression for the Freundlich isotherm can be represented by the following equation;
$\Rightarrow \dfrac{x}{m}=k{{P}^{\dfrac{1}{n}}}$
Where $x$ is the mass of the gas adsorbed, $m$is the mass of the adsorbent, $P$ is the pressure and $n$ is a constant which depends upon the nature of adsorbent and the gas at a given temperature. Taking the logarithm on both the sides of the equation, we get;
$\Rightarrow \log \dfrac{x}{m}=\log k+\dfrac{1}{n}\log {{P}^{{}}}$
On comparing this equation with the equation of straight line($y=mx+c$). The plot of this equation is a straight line as represented by the following curve.

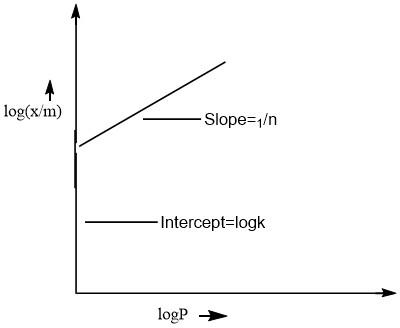
From the graph, it is very clear that only $1/n$ appears as the slope.

So, the correct answer is Option B.

Note: The Freundlich adsorption isotherm is followed by another two isotherms, Langmuir adsorption isotherms and BET theory. The Langmuir adsorption isotherms predict linear adsorption at low adsorption densities and a maximum surface coverage at higher solute metal concentrations.