Solveeit Logo
Login

Question

Question: For a lezim kawayat the girls of standard IX are arranged in two circular concentric rings as shown ...

For a lezim kawayat the girls of standard IX are arranged in two circular concentric rings as shown in the figure. If PA=15m, PR=25m, QR=10m then find the measures of RS, PQ, and QT.

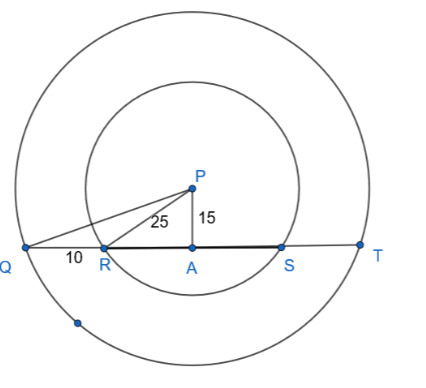
(a) 40m,155m,and60m,40m,15\sqrt 5 m,and60m,
(b) 20m,305m,and60m,20m,30\sqrt 5 m,and60m,
(c) 40m,155m,and30m,40m,15\sqrt 5 m,and30m,
(d) 10m,305m,and60m,10m,30\sqrt 5 m,and60m,

Explanation

Solution

Hint:We can use the Pythagoras theorem, which states the relation between base, perpendicular, and hypotenuse.
(base)2+(perpendicular)2=(hypotenuse)2{{\left( base \right)}^{2}}+{{\left( perpendicular \right)}^{2}}={{\left( hypotenuse \right)}^{2}}

Complete step by step answer:
We can see in the figure that triangle ARP is right-angled at A. So, we can apply Pythagoras Theorem here to find out the value of AR.
(15)2+(AR)2=(25)2{{\left( 15 \right)}^{2}}+{{\left( AR \right)}^{2}}={{\left( 25 \right)}^{2}}
Now, we will simplify the above equation to find the value of AR.
⇒(AR)2=(25)2−(15)2\Rightarrow {{\left( AR \right)}^{2}}={{\left( 25 \right)}^{2}}-{{\left( 15 \right)}^{2}}
⇒(AR)2=625−225=400\Rightarrow {{\left( AR \right)}^{2}}=625-225=400
⇒AR=20\Rightarrow AR=20
So, we have now found the value of the length of line segment AR.
Also, we also know that perpendicular from the center to a chord bisects the chord.
So, we can find out the length of the line segment RS.
RS=2(AR)=40m..................(i)RS=2\left( AR \right)=40m..................(i)
Since we are already provided with the length of line segment QR, we can find out the length of the line segment AQ.
AQ=AR+QR
⇒AQ=20+10=30m..................(ii)\Rightarrow AQ=20+10=30m..................(ii)
Now, we can see that the triangle PAQ is also right-angled at A.
(15)2+(AQ)2=(PQ)2{{\left( 15 \right)}^{2}}+{{\left( AQ \right)}^{2}}={{\left( PQ \right)}^{2}}
⇒(PQ)2=152+302=900+225=1125\Rightarrow {{\left( PQ \right)}^{2}}={{15}^{2}}+{{30}^{2}}=900+225=1125
⇒PQ=155m....................(iii)\Rightarrow PQ=15\sqrt{5}m....................(iii)
Again, we are left only with QT to be found. We can see that AP is bisecting the line segment QT. So, we can find the length of the line segment QT by doubling the QA.
QT=2(QA)
⇒QT=2(30)=60m......................(iv)\Rightarrow QT=2(30)=60m......................(iv)
So, we have found out the value of RS, PQ, QT.
RS=40m
PQ=155mPQ=15\sqrt{5}m
QT=60m
Hence, option (a) is correct.

Note: We have to be aware of identifying the hypotenuse. One common mistake is that while writing the Pythagoras Theorem, one needs to identify the right angle and write the hypotenuse. A common method to memorize is that the side opposite to the right angle is the hypotenuse.