Question

For a hydrogenic quantum system, the probability of finding the electron $D_{n,l}(r)dr$ in a spherical shell of radius $r$ (with nucleus at its center) and thickness $dr$, is plotted against $r$ (in units of $a_0$) for three sets of values of $n$ and $l$ (plots I, II, and III). The principal quantum number $(n)$, azimuthal quantum number $(l)$ and area under the curve $(A)$ corresponding to the three plots are denoted by subscripts I, II, and III respectively. (The plots are not drawn to scale.)

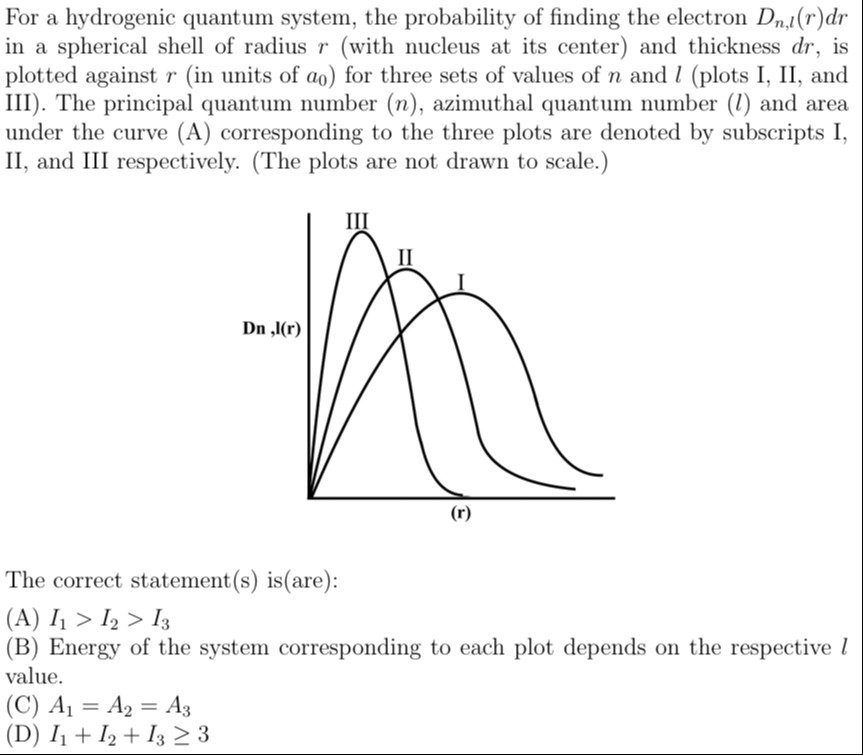
• A. $I_1 > I_2 > I_3$
• B. Energy of the system corresponding to each plot depends on the respective $l$ value.
• C. $A_1 = A_2 = A_3$
• D. $I_1 + I_2 + I_3 \ge 3$

Answer 1

Answer: (A), (C), (D)

A, C, D

Answer 2

The problem describes the radial probability distribution $D_{n,l}(r)$ for a hydrogenic quantum system. We are given three plots (I, II, III) showing $D_{n,l}(r)$ versus $r$. We need to identify the correct statement(s) regarding the principal quantum number $(n)$, azimuthal quantum number $(l)$, and the area under the curve $(A)$ for these plots.

Understanding the Radial Probability Distribution $D_{n,l}(r)$:

$D_{n,l}(r)dr$ is the probability of finding the electron in a spherical shell of radius $r$ and thickness $dr$. The function $D_{n,l}(r)$ is given by $4\pi r^2 R_{n,l}(r)^2$, where $R_{n,l}(r)$ is the radial part of the wave function.

Analyzing the Plots:

1. Number of Peaks/Nodes: Each plot (I, II, III) shows a single peak and starts from zero at $r=0$. This shape is characteristic of orbitals with no radial nodes. The number of radial nodes is given by $n - l - 1$. If there are no radial nodes, then $n - l - 1 = 0$, which means $l = n-1$. Examples of such orbitals are 1s ($n=1, l=0$), 2p ($n=2, l=1$), 3d ($n=3, l=2$), 4f ($n=4, l=3$), etc.

2. Position of Peaks: From the graph, the most probable radius (the position of the peak) for the three plots follows the order: $r_{peak, I} > r_{peak, II} > r_{peak, III}$. For hydrogenic atoms, the most probable radius for orbitals with $l=n-1$ is approximately proportional to $n^2$. Specifically, $r_{mp} = \frac{n^2 a_0}{Z}$. Therefore, $n_I^2 > n_{II}^2 > n_{III}^2$, which implies $n_I > n_{II} > n_{III}$.

Evaluating the Options:

(A) $I_1 > I_2 > I_3$

The problem states that $n, l, A$ for the three plots are denoted by subscripts I, II, III. So, $I_1, I_2, I_3$ in the options refer to $n_I, n_{II}, n_{III}$ respectively. Based on our analysis of the peak positions and the characteristic of orbitals with no radial nodes, we concluded that $n_I > n_{II} > n_{III}$. Thus, statement (A) is correct.

(B) Energy of the system corresponding to each plot depends on the respective $l$ value.

For a hydrogenic quantum system (like H, He+, Li2+), the energy of an electron in a given orbital depends only on the principal quantum number $n$. The formula for energy is $E_n = -\frac{Z^2 R_H}{n^2}$, where $R_H$ is the Rydberg constant. The energy is independent of the azimuthal quantum number $l$. Thus, statement (B) is incorrect.

(C) $A_1 = A_2 = A_3$

The area under the radial probability distribution curve $D_{n,l}(r)$ from $r=0$ to $r=\infty$ represents the total probability of finding the electron in all of space. Since the electron must be found somewhere, this total probability must be equal to 1 for any normalized wave function. $\int_0^\infty D_{n,l}(r) dr = 1$ Therefore, the area under each plot ($A_I, A_{II}, A_{III}$) must be equal to 1. Thus, $A_I = A_{II} = A_{III}$. Statement (C) is correct.

(D) $I_1 + I_2 + I_3 \ge 3$

Assuming $I_1, I_2, I_3$ refer to $n_I, n_{II}, n_{III}$ respectively. From the analysis of (A), we established $n_I > n_{II} > n_{III}$. Since $n$ is a principal quantum number, its minimum value is 1. For distinct $n$ values following the order $n_I > n_{II} > n_{III}$, the smallest possible integer values are $n_{III}=1$, $n_{II}=2$, and $n_I=3$. In this case, $n_I + n_{II} + n_{III} = 3 + 2 + 1 = 6$. Since $6 \ge 3$, the statement $n_I + n_{II} + n_{III} \ge 3$ is correct.

Based on the analysis, statements (A), (C), and (D) are correct.