Question
Question: For a given square matrix P, of order q, if $|adj(P)|=|P|^k$, what is the value of k?...
For a given square matrix P, of order q, if ∣adj(P)∣=∣P∣k, what is the value of k?
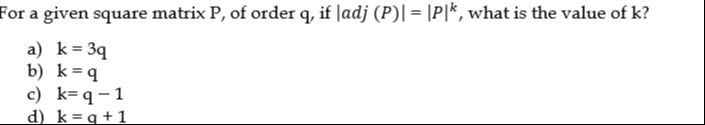
k = 3q
k = q
k = q - 1
k = q + 1
k = q - 1
Solution
To find the value of k for a given square matrix P of order q, such that ∣adj(P)∣=∣P∣k, we use the fundamental property relating a matrix, its adjoint, and its determinant.
1. Fundamental Property of Adjoint Matrix:
For any square matrix P of order q, the product of the matrix and its adjoint is equal to the determinant of the matrix times the identity matrix of the same order:
P⋅adj(P)=∣P∣Iq
where Iq is the identity matrix of order q.
2. Taking Determinant on Both Sides:
Now, we take the determinant of both sides of the equation:
∣P⋅adj(P)∣=∣∣P∣Iq∣
3. Applying Determinant Properties:
We use two properties of determinants:
- ∣AB∣=∣A∣∣B∣ for square matrices A and B.
- ∣cA∣=cn∣A∣ for a scalar c and a square matrix A of order n. In our case, A=Iq and n=q. Also, ∣Iq∣=1. So, ∣∣P∣Iq∣=(∣P∣)q∣Iq∣=(∣P∣)q⋅1=(∣P∣)q.
Applying these properties to our equation:
∣P∣⋅∣adj(P)∣=(∣P∣)q
4. Substituting the Given Relation:
We are given that ∣adj(P)∣=∣P∣k. Substitute this into the equation:
∣P∣⋅∣P∣k=(∣P∣)q
5. Simplifying the Equation:
Using the rule of exponents am⋅an=am+n:
∣P∣1+k=∣P∣q
6. Solving for k:
This equation holds true for all square matrices.
- Case 1: If ∣P∣=0 (P is a non-singular matrix):
If the base ∣P∣ is non-zero, we can equate the exponents:
1+k=q
k=q−1
- Case 2: If ∣P∣=0 (P is a singular matrix):
The equation becomes 01+k=0q.
If q>1, then q−1>0. In this case, 0q=0 and 01+k=0 (since 1+k=q>0). So, 0=0, which is consistent with k=q−1.
The only exception is for q=1 and ∣P∣=0. For a 1×1 matrix P=[0], adj(P)=[1]. So ∣adj(P)∣=1. The given relation becomes 1=0k, which is impossible for any k. However, such questions typically refer to the general property derived from the non-singular case, which is universally accepted in matrix theory.
Therefore, the value of k that satisfies the relation for a general square matrix is k=q−1.
