Question

For a given optical system, the principal axis is the x-axis, and coordinates of the object are $\left( { - 30, + 1,0} \right)$ and coordinates of the image are $\left( { + 20, - 2,0} \right)$ . (All coordinates are in cm.) If the optical system is a convex lens, what is its focal length?
A) 12 cm
B) 10 cm
C) $100/3\,cm$
D) $100/9\,cm$

Answer 1

Hint : In this solution, we will use the relation of magnification of an image after refraction to find the image and object distance from the lens. We will then use the lens formula to find the focal length of the lens

Formula used: In this solution we will be using the following formula,
Magnification of a lens: $m = - \dfrac{v}{u} = \dfrac{{{h_i}}}{{{h_o}}}$ where $v$ is the object distance, $u$ is the image distance, ${h_i}$ is the image height, and ${h_o}$ is the object height
Lens formula: $\dfrac{1}{v} - \dfrac{1}{u} = \dfrac{1}{f}$ where $v$ is the image distance, $u$ is the object distance, and $f$ is the focal length of the lens

Complete step by step answer
We’ve been given that for our optical system, coordinates of the object are $\left( { - 30, + 1,0} \right)$ and coordinates of the image are $\left( { + 20, - 2,0} \right)$ . The ray diagram of this system is shown below.
The distance between the image and the object is $= 20 - ( - 30) = 50\,cm$
Let us assume the object distance as $u = - x$ . Hence the image distance will be $v = 50 - x$

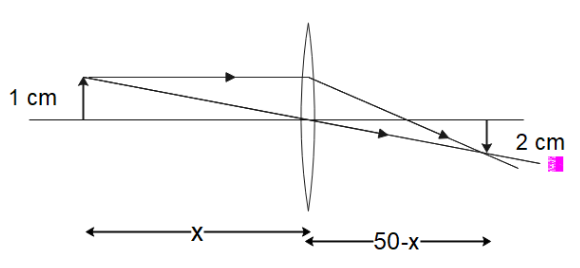
We know that the magnification of a lens can be written as
$\Rightarrow m = - \dfrac{v}{u} = \dfrac{{{h_i}}}{{{h_o}}}$
Since ${h_i} = 2\,{\text{and}}\,{{\text{h}}_o} = 1$ , we can write
$\Rightarrow \dfrac{{50 - x}}{x} = \dfrac{2}{1}$
Cross multiplying the denominators, we get
$\Rightarrow 50 - x = 2x$
$\Rightarrow x = 50/3$
So $u = - x = - 50/3$ and $v = 50 - x = 100/3$ . We can now use the lens formula
$\Rightarrow \dfrac{1}{v} - \dfrac{1}{u} = \dfrac{1}{f}$
Substituting the proper values, we get
$\Rightarrow \dfrac{1}{{\dfrac{{100}}{3}}} + \dfrac{1}{{\dfrac{{50}}{3}}} = \dfrac{1}{f}$
$\Rightarrow \dfrac{1}{f} = \dfrac{9}{{100}}$
On taking the inverse,
$f = \dfrac{{100}}{9}\,cm$ which corresponds to option (D).

Note
While using the lens formula, we must be careful of the sign conventions of the image and object distance as the object is on the left and it will have a negative object distance and the image is on the right and it has a positive image distance. Since this is a convex lens, the focal length of the lens will always be positive.