Question

For a given circuit it is observed that the current $I$ is independent of the value of the resistance ${R_6}$ . The resistance values must satisfy:

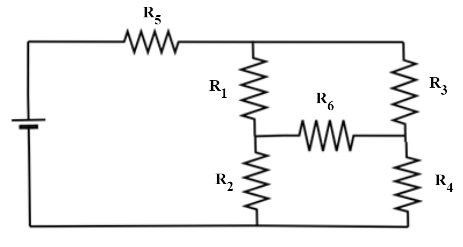
A. ${R_2}{R_3} = {R_1}{R_4}$
B. ${R_3}{R_4}{R_6} = {R_2}{R_1}{R_5}$
C. $\dfrac{1}{{{R_3} + {R_4}}} = \dfrac{1}{{{R_5} + {R_6}}} = \dfrac{1}{{{R_1} + {R_2}}}$
D. ${R_3}{R_1} = {R_2}{R_4} = {R_5}{R_6}$

Answer 1

To find the condition that satisfy the circuit in which the current $I$ is independent of the value of the resistance ${R_6}$ , i.e. no current should be flowing through ${R_6}$ , we analyze the junctions of the same potential. We use the concept of Wheatstone’s meter bridge to find the condition.

Complete step by step answer:
We know that, current $I$ is independent of the value of the resistance ${R_6}$ , no current is flowing through the ${R_6}$. This requires that the junction of ${R_1}\& {R_2}$ must be at the same potential as the junction of ${R_3}\& {R_4}$. This must satisfy the Wheatstone’s meter bridge balancing condition i.e. ${R_2}{R_3} = {R_1}{R_4}$.

Hence, option A is correct.

Note: The Wheatstone’s meter bridge is an arrangement of four resistances used to measure one of them in terms of the three. We should note that, on changing the position of the cell and resistances, the balancing condition is not changed. Resistance ${R_5}$ is in series with ${R_1}$, so it will not produce any effect in the balancing condition.