Question

For a gas obeying P (V-b) = RT a graph is placed between Volume (V lit.) on Y-axis and Temperature (K) on X-axis at a constant pressure of 0.04105 atm. Find the slope of the line?

Answer 1

To find the slope, the term on the y axis has to be made subjective and the equation has to be derived just like $y=mx+c$. Thus, after adjustments in the above-given equation, the term we find in place of m has to be the slope of the line.

Complete answer:
The slope for the line plotted for P (V-b) = RT, when the pressure is kept constant, is $\dfrac{R}{P}$ .
As it is given in the question that volume is plotted on the y-axis and temperature is plotted on the x-axis, we can make volume as a subject and try to obtain a simple equation like y=mx+c.
Also, the pressure is kept constant, thus it can be included in the slope.
To make (V-b) the subject, the first pressure is taken to the denominator on the other side.
$V-b=\dfrac{RT}{P}$
Making volume the subject, we get
$V=\dfrac{RT}{P}+b$
Thus, this equation is similar to y=mx+c. Now let’s compare both the equations, the volume becomes y, $\dfrac{R}{P}$ becomes m, temperature becomes x and b becomes c. Thus as m is the slope, $\dfrac{R}{P}$ becomes the slope.
Therefore, $m=\dfrac{R}{P}$ .
As R is the universal gas constant, we can assume its value as 0.0821, and we have been given the value of pressure.
Thus, $m=\dfrac{0.0821}{0.04105}$ .
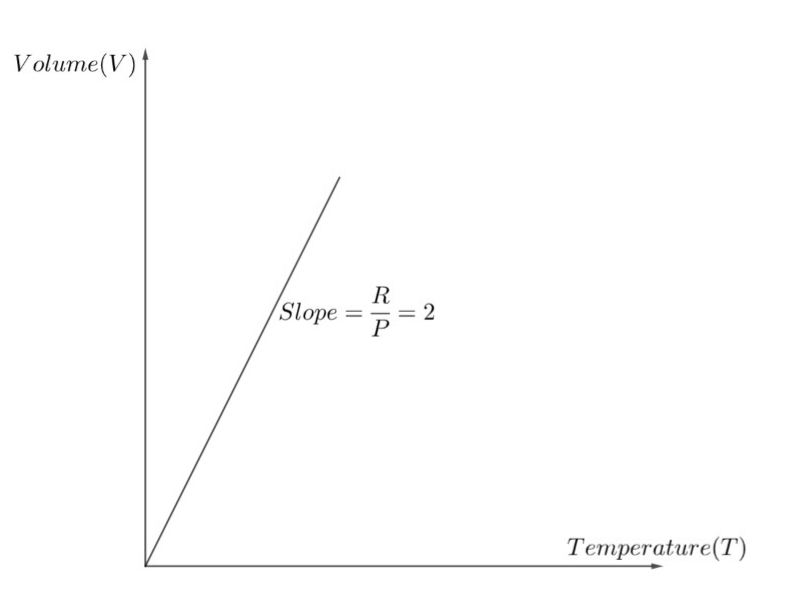
Thus, m = 2. Thus the value of the slope is 2. And the general formula for the slope in this question is $m=\dfrac{R}{P}$ .
The graph of the slope is shown below.

Note:
It is important to remember that the value assigned on the y-axis keeps in the place of y in the equation $y=mx+c$, if this is not done properly we cannot find the slope of the line correctly. Also, the value of the universal gas constant should be known as it is useful for these types of questions.