Solveeit Logo
Login

Question

Question: For a concave mirror, the paraxial rays are focused at distance \(\dfrac{R}{2}\) from pole and margi...

For a concave mirror, the paraxial rays are focused at distance R2\dfrac{R}{2} from pole and marginal rays are focused at distance x from pole, then?(R is radius of curvature)
a)x=R2 b)x=−f c)x>R2 d)x<R2 \begin{aligned} & a)x=\dfrac{R}{2} \\\ & b)x=-f \\\ & c)x>\dfrac{R}{2} \\\ & d)x<\dfrac{R}{2} \\\ \end{aligned}

Explanation

Solution

In the question it is given to us the paraxial rays pass through the distance R2\dfrac{R}{2} from the pole of the concave mirror. The answer to the above question can easily be generated, as the marginal rays suffer more deviation than the paraxial rays. Hence we will see how the deviation of the rays makes the change the position of the paraxial and the marginal rays from the pole of the concave mirror.

Complete answer:
To begin with let us first understand what does marginal and paraxial rays mean. Paraxial rays are nothing but a set of incident rays on the mirrors which lie very close to the principal axis. Whereas marginal rays are the set of incident rays of light on the mirror that hit the mirror towards its edges with respect to the pole of the mirror. Figure below explains this scenario.

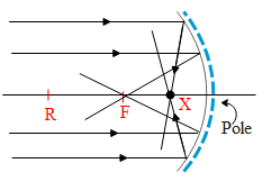
The marginal rays suffer more deviation as compared to the paraxial rays. Hence we can see that both the set of rays meet at different points on the principal axis. The rays close to the principal axis i.e. are the paraxial rays after reflection from the concave mirror meet at the focus (f)i.e. f=R2f=\dfrac{R}{2}. Since the marginal rays suffer more deviation i.e. with respect to their normal of incidence they are incident at greater angles with respect to the paraxial rays. Hence they meet somewhere between the focus and the pole of the mirror. Hence we can conclude that the distance of the point where the marginal rays meet the principal axis, is smaller than that of the paraxial rays meeting the focus. If x is the point where the marginal rays meet, then we can say that x<R2x<\dfrac{R}{2}

Therefore the correct answer of the above question is option d.

Note:
It is to be noted this process is called spherical aberration. The cause of spherical aberration is nothing but the aperture of the spherical mirrors. If the above condition is overcome, then we can say that the spherical mirrors will have the least spherical aberration.