Question
Question: For a closed (not rigid ) container containing \(n = 10\) moles of an ideal gas fitted with a movabl...
For a closed (not rigid ) container containing n=10 moles of an ideal gas fitted with a movable, frictionless, weightless piston operating such that pressure of gas remains constant at 0.821atm.Which graph represents a correct variation of log V vs log T where V is in litre and T in Kelvin?
A)
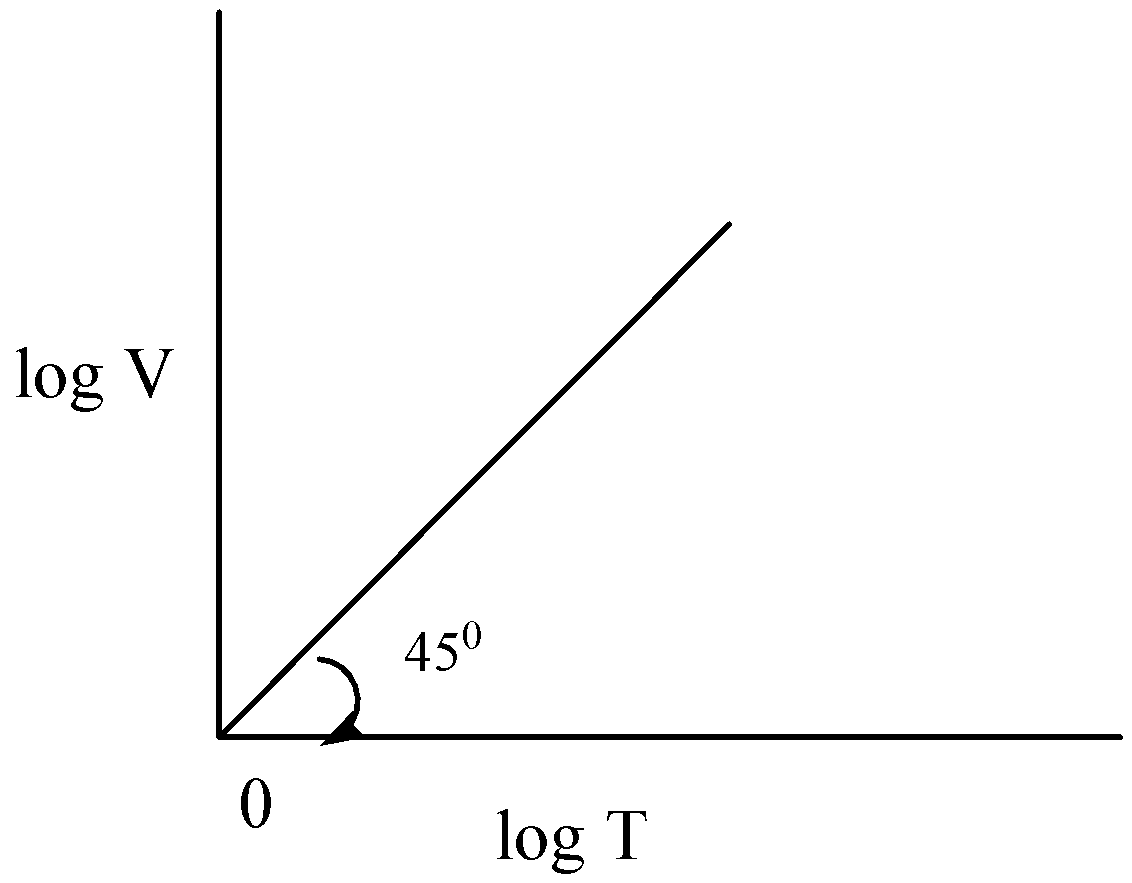
B)
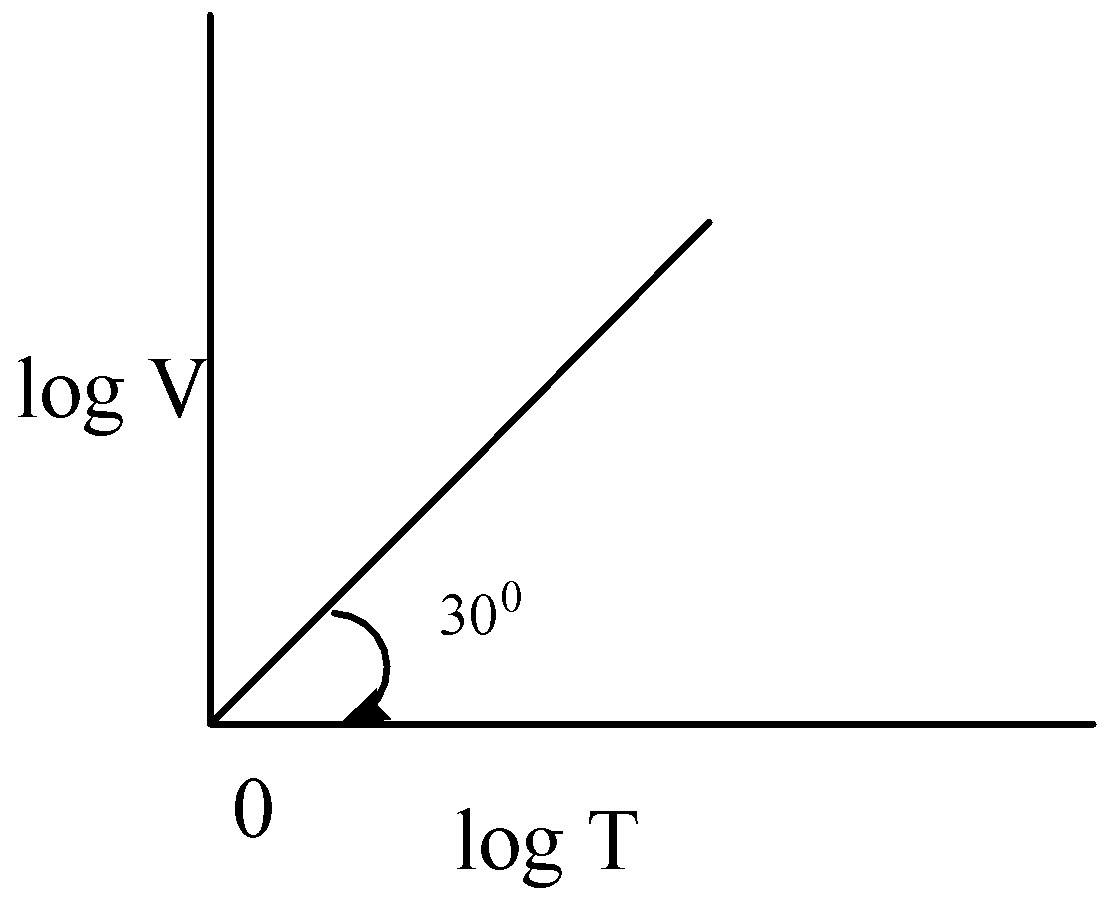
C)
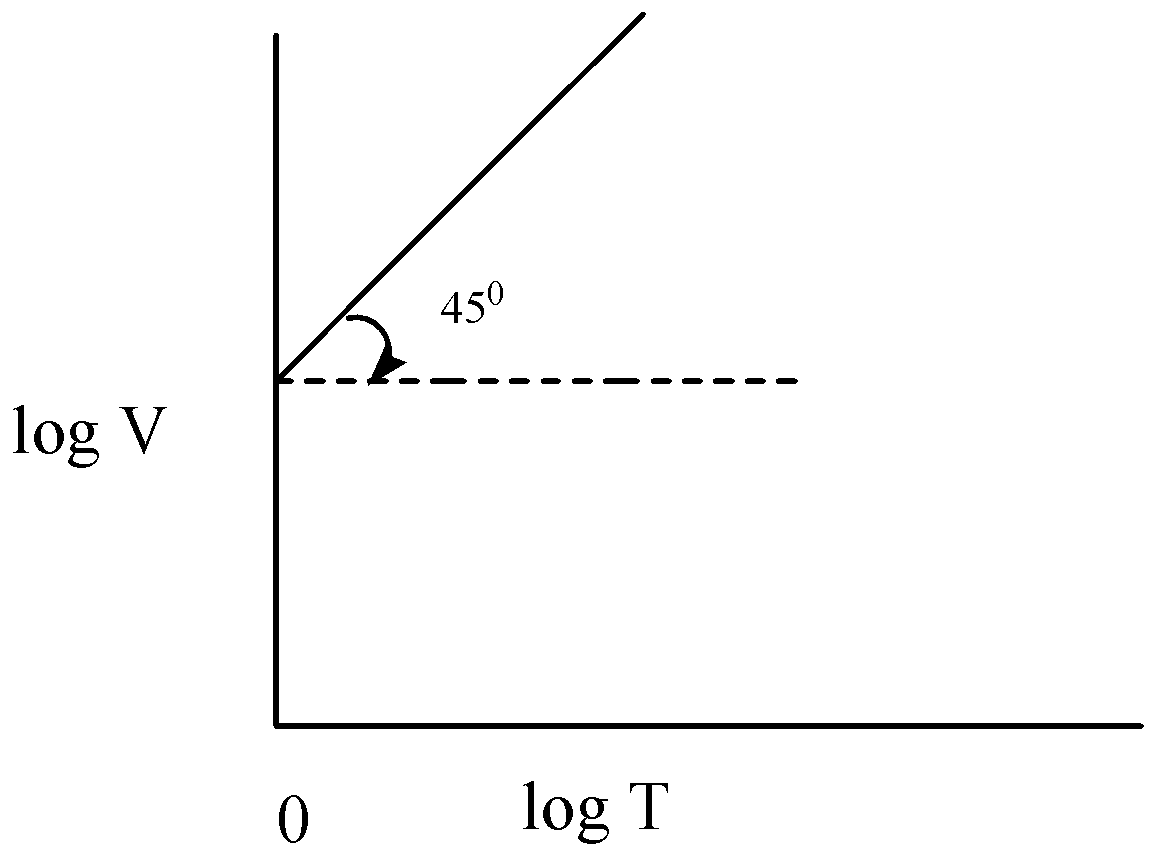
D)
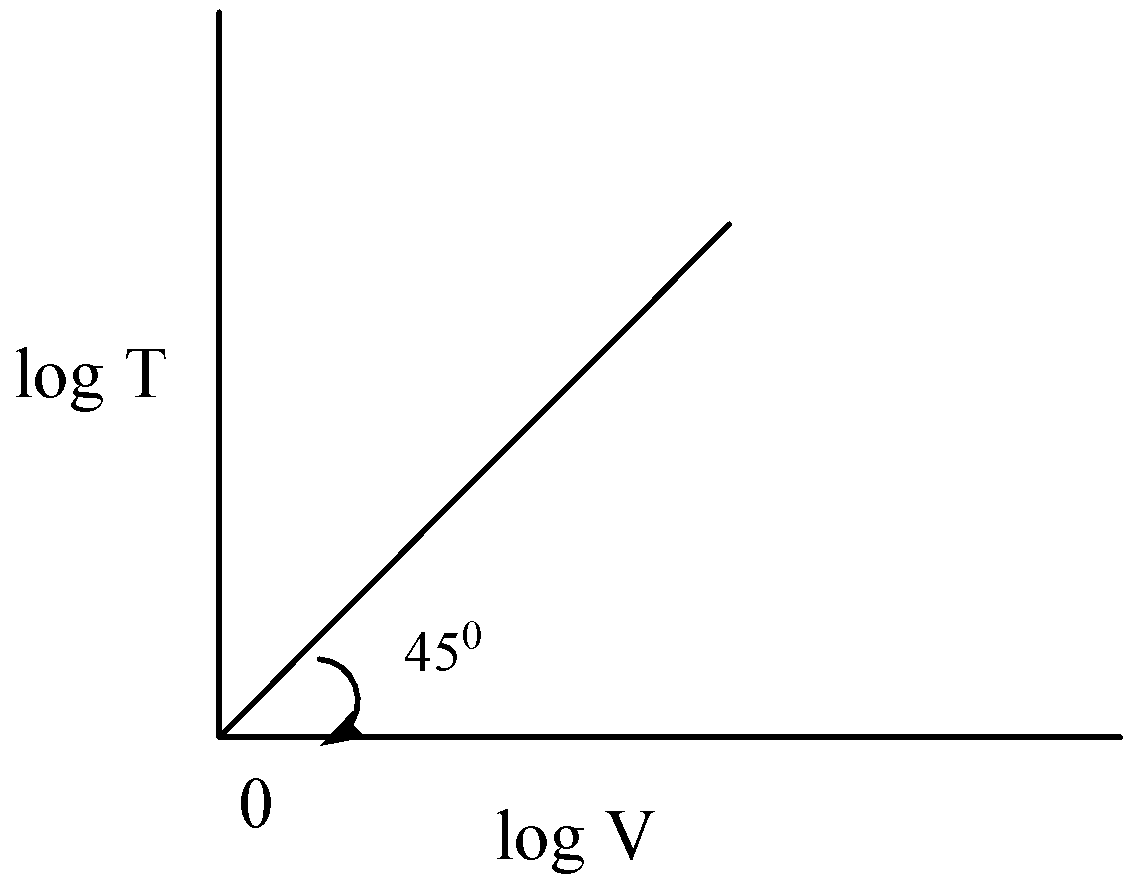
Solution
We know that the ideal gas law is the condition of a speculative ideal gas. It is a decent estimation of the conduct of numerous gases under numerous conditions, despite the fact that it has a few impediments
The ideal gas equation is,
PV=nRT
Where P is the pressure in the atmosphere.
V is the volume of gas in a liter.
n is the number of moles.
R is a universal gas constant.
T is the temperature.
Complete step by step answer:
Given,
The number of moles n=10.
The pressure of gas is 0.821atm.
The value of gas constant is 0.0821Latmmol−1K−1.
We know the ideal gas equation is,
PV=nRT
Now, substitute the known qualities in the above condition,
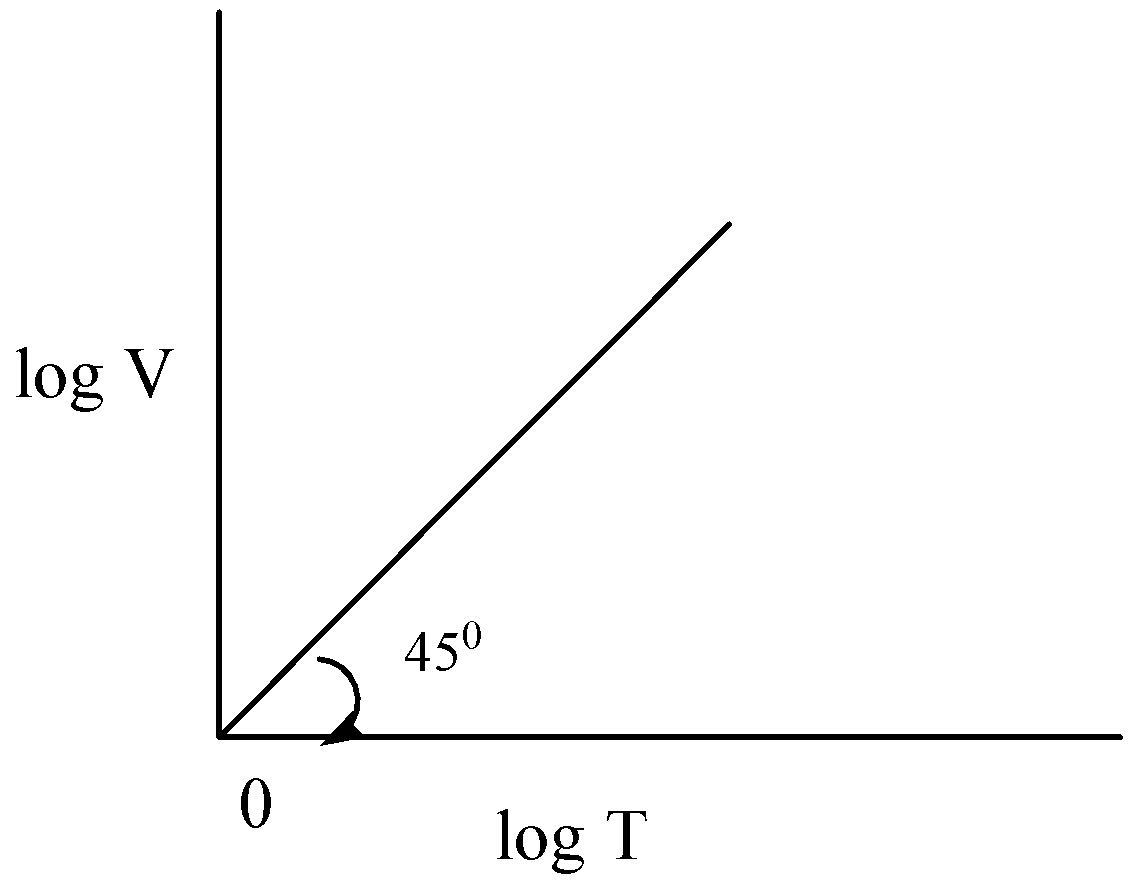
V=0.82110×0.0821×T
V=1×T
logTlogV=1
tanθ=1
tan45∘=1
Hence option A is correct.
Additional information:
If the gas obeys an ideal gas equation then the pressure is given by,
P = VnRT→1
If the volume is doubled and the temperature is halved then the equation becomes,
P = 2VnRT/2
P = 4VnRT→2
From equation 1 P = VnRT then the equation 2 becomes,
P = 4P
Thus, if the volume is doubled and the temperature is halved then the pressure of the system decreases by four times.
Note:
We know that,
Density = volumemass
Assuming mass is equal to the number of moles in ideal gas.
Density = volumen
The ideal gas equation is,
PV = nRT
The number of moles can be calculated as,
n = RTPV
Substituting the value of n in density equation,
Density = RTVPV
Density = RTP
Density∝T1
It is clear that density is inversely proportional to temperature. Thus, as the density of the gas decreases temperature increases.
