Question

For a circle ${{x}^{2}}+{{y}^{2}}+2gx+c=0$, to have limiting points:
(A). $g=c$
(B). $g={{c}^{2}}$
(C). $g=\pm \sqrt{c}$
(D). None of these

Answer 1

Hint: The limiting points of a family of circles is the point at which the radius of the circle becomes zero. It essentially is a point circle, but since the radius of a point circle is zero, the centre of the point circle is the same as any other point on its circumference, and this point is known as the limiting point. So, in this question, all you have to do is make the radius zero.

Complete step-by-step solution -
The equation given to us here : ${{x}^{2}}+{{y}^{2}}+2gx+c=0$ is the equation of a family of circles. This is because, here, $g$ is a variable, and it can have an infinite number of values. This will thus, result in the existence of an infinite number of circles, all of which satisfy the given equation. All the circles that satisfy the given equation, together, is known as a family of circles with the general equation as ${{x}^{2}}+{{y}^{2}}+2gx+c=0$.
Here’s a diagram illustrating the concept of family of circles better :

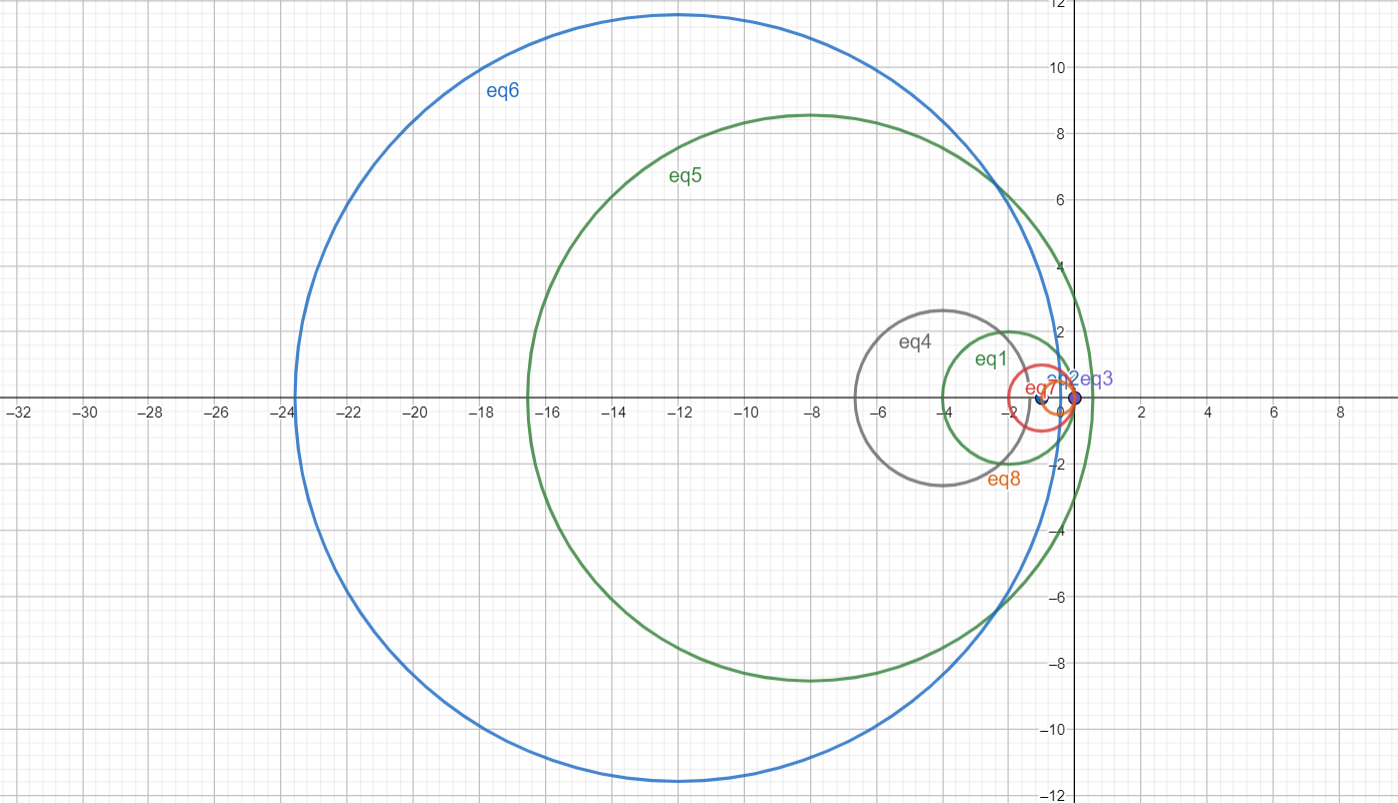
The limiting point of a family of circles is known as the circle, belonging to this family, whose radius is zero. Since in our given equation, $c$ is also a variable, each of the circles can have any radius possible, depending on the value of $c$, since the radius of a circle = $\sqrt{{{g}^{2}}+{{f}^{2}}-c}$.
Thus, to find the limiting point of the family of circles represented by the equation ${{x}^{2}}+{{y}^{2}}+2gx+c=0$, we need to find that circle, whose radius will be equal to $0$. That circle, since its radius is zero, will basically be a point, or can even be called a point circle, and hence, that particular point is called a limiting point of that particular family of circles.
Hence, our aim should be to equate the radius of the circle to $0$.
$\begin{aligned} & \Rightarrow radius=0 \\\ & \Rightarrow \sqrt{{{g}^{2}}+{{f}^{2}}-c}=0 \\\ \end{aligned}$
The given circle is ${{x}^{2}}+{{y}^{2}}+2gx+c=0$. Comparing it with the general form of the circle ${{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0$, we see that the equation ${{x}^{2}}+{{y}^{2}}+2gx+c=0$ has no variable “y” in it.
Therefore, we have,
$\begin{aligned} & 2f=0 \\\ & \Rightarrow f=0 \\\ \end{aligned}$
Now, for radius to be equal to zero, $\sqrt{{{g}^{2}}+{{f}^{2}}-c}=0$ .
$\Rightarrow \sqrt{{{g}^{2}}+0-c}=0$
$\Rightarrow \sqrt{{{g}^{2}}-c}=0$
On squaring both sides, we get ${{g}^{2}}-c=0$ .
$\Rightarrow {{g}^{2}}=c$
$\Rightarrow g=\pm \sqrt{c}$
Hence, the condition of limiting point is satisfied merely by $g=\pm \sqrt{c}$ and this is our answer, option (c).

Note: All the circles shown in the diagram of a family of circles belong to the family represented by the equation ${{x}^{2}}+{{y}^{2}}+2gx+c=0$ since all the values of $g$ and $c$ in these circles are acceptable. The number of values $g$ and $c$ can take is infinite, and there definitely are more circles belonging to this particular family as well.