Question

Following figures show the arrangement of bar magnets in different configurations. Each magnet has a magnetic dipole moment $\vec{m}$. Which configuration has the highest net magnetic dipole moment?

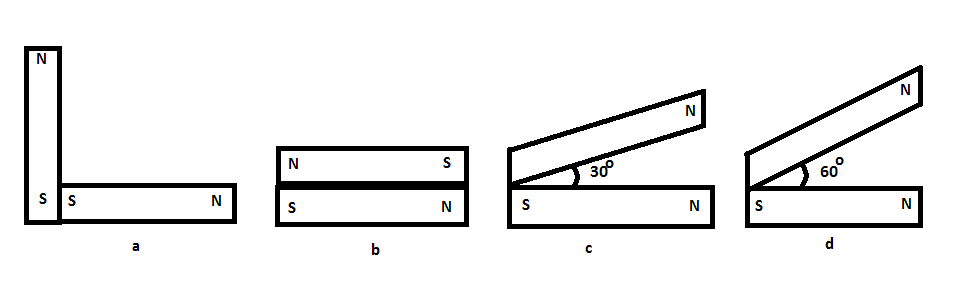
A $a$
B $b$
C $c$
D $d$

Answer 1

Here, each bar magnet has a magnetic dipole moment as $\vec{m}$. Since magnetic dipole moment is a vector quantity, we can find the resultant magnetic dipole moment using the formula for finding magnitude of a vector quantity. Thus
we can determine which configuration has the highest net magnetic moment.
Formula used:
${{m}_{net}}=\sqrt{{{m}_{1}}^{2}+{{m}_{2}}^{2}+2{{m}_{1}}{{m}_{2}}cos\theta }$

Complete step-by-step solution:
Given that, each bar magnet has a magnetic dipole moment $\vec{m}$. Magnetic dipole moment has its direction from north to south. Now let’s find out the net magnetic dipole moment of each configuration using a vector diagram.
In the first configuration, bar magnets have an angle ${{90}^{0}}$ between them. The resultant vector will be in a ${{45}^{0}}$ angle with both the magnets.

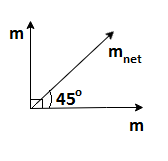
Magnitude of a vector m can be found using the formula,
${{m}_{net}}=\sqrt{{{m}_{1}}^{2}+{{m}_{2}}^{2}+2{{m}_{1}}{{m}_{2}}cos\theta }$
Then,
${{m}_{net}}=\sqrt{{{m}^{2}}+{{m}^{2}}+2{{m}^{2}}\cos 90}=\sqrt{2}m$
In the second configuration, the bar magnets are parallel to each other.

Hence,
${{m}_{net}}=m-m=0$
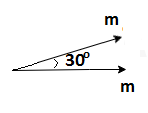
In the third configuration, magnets have a $30{}^\circ$ angle between them.

30}=m\sqrt{3.732}=1.93m$$ In the fourth configuration, magnets have $$60{}^\circ $$ angle between them.  $${{m}_{net}}=\sqrt{{{m}^{2}}+{{m}^{2}}+2{{m}^{2}}\cos 60}=m\sqrt{3}=1.732m$$ **Hence, configuration $$c$$ has the highest net magnetic dipole moment. Answer is option C** **Additional information:** Consider a magnetic dipole with two equal and opposite magnetic charges of strengths $$+m$$ and $$-m$$ and separated by a distance $$2l$$. Then, its magnetic dipole moment can be given by, $$M=m\times 2l$$ **Note:** A bar magnet is usually considered as a dipole with dipole moment$$\vec{m}$$. Magnetic dipole moment is a vector quantity and has direction from $$-m$$ to $$+m$$. Its S.I unit is $$\text{Ampere }{{\text{m}}^{\text{2}}}$$.