Question
Question: Focal length of the convex lens is \[3cm\] . Find the image distance if an object of height \[2cm\] ...
Focal length of the convex lens is 3cm . Find the image distance if an object of height 2cm is placed at 7cm from the lens?
Solution
In order to answer the given question where we are asked to find out the image distance we will use the lens formula. The lens formula is a relationship between a lens' focal length and the distance between an object in front of it and the image created by that object.
Formula used:
f1=v1−u1
Where,
v− is the image distance
u− is the object distance
f− is the focal length
Complete step by step solution:
The Lens formula describes the relationship between the distance of an image (v) , the distance of an object (u) , and the focal length (f) of the lens in optics. The lens formula works for both convex and concave lenses. The thickness of these lenses is minimal. The following is the formula: f1=v1−u1
To determine the desired answer to our supplied question, we will use the formula above.
The focal length as (3cm) and the object distance as (−7cm) is given to us in the question hence, we need to find out the image distance. So,
The ray diagram of image formation is given by
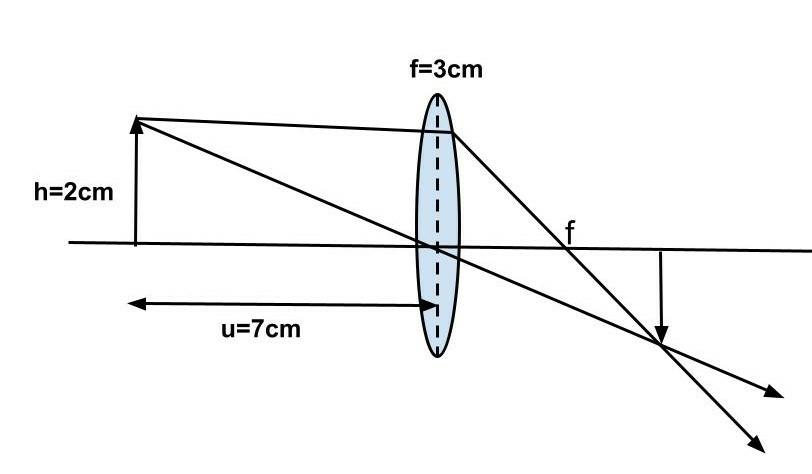
f1=v1−u1
Where, (u=−7,f=3cm)
Now, arranging the equation in manner
f1+u1=v1
Now, putting all the known terms
31−71=v1
Now, taking LCM
217−3=v1 214=v1 ∴v=421=5.25cm
Therefore the image distance will be 5.25cm .
Note:
The lens formula is applicable to both convex and concave lenses. It can also be used to figure out how far real and virtual images are apart. If the equation yields a negative image distance, the resulting picture is virtual and on the same side as the item. If the equation yields a negative focal length, the lens is diverging rather than converging.
