Question

Flux($\phi$) of curved surface?

Answer 1

Using Gauss law you could find the net flux through the given cylinder. Since we are asked to find the flux through the curved surface specifically, we could subtract the flux through the two flat surfaces from the total flux. We know that the expression for solid angle made by the cone with half angle $\theta$ and also remember that flux for solid angle $4\pi$ is the total flux$\dfrac{q}{{{\varepsilon }_{0}}}$. Using all these points find the required flux.

Formula used:
Gauss’s law,
$\phi =\dfrac{1}{{{\varepsilon }_{0}}}\left( {{q}_{en}} \right)$

Complete step by step solution:
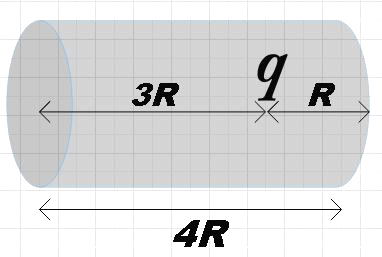
We are given a closed cylinder of radius R and length 4R inside which a charge q is kept at distance 3R from one end and distance R from the other end. We are asked to find the electric flux that passes through the curved surface of the given cylinder.
From Gauss’s law we know that the total flux of a closed surface is $\dfrac{1}{{{\varepsilon }_{0}}}$ times the charge enclosed by the closed surface. That is, if ${{\phi }_{t}}$ is the total flux associated with a closed surface then,
${{\phi }_{t}}=\dfrac{1}{{{\varepsilon }_{0}}}\left( q \right)$ …………………………….. (1)
So, the total flux associated with the given cylinder will also be the same. But, we are asked specifically to find the flux through the curved surface, for that, we have to subtract the flux through both the flat faces from this total.
Let ${{\phi }_{1}}$ and ${{\phi }_{2}}$ be the flux through the flat surfaces at distance 3R and R respectively, then, flux $\phi$ through the curved surface is given by,
$\phi ={{\phi }_{t}}-\left( {{\phi }_{1}}+{{\phi }_{2}} \right)$ ………………………………….. (2)

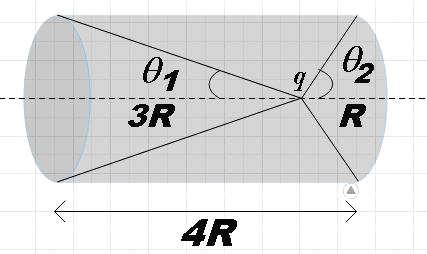
From the figure we see that,
$\cos {{\theta }_{1}}=\dfrac{3R}{\sqrt{{{R}^{2}}+{{\left( 3R \right)}^{2}}}}$
$\Rightarrow \cos {{\theta }_{1}}=\dfrac{3R}{\sqrt{10}R}$
$\therefore \cos {{\theta }_{1}}=\dfrac{3}{\sqrt{10}}$ ……………………………….. (3)
Similarly,
$\cos {{\theta }_{2}}=\dfrac{R}{\sqrt{{{R}^{2}}+{{R}^{2}}}}$
$\therefore \cos {{\theta }_{2}}=\dfrac{1}{\sqrt{2}}$ ………………………………... (4)
Now the solid angle made by the cone of half angle $\theta$ at the point at which q is kept is given by,
$\Omega =2\pi \left( 1-\cos \theta \right)$ …………………………… (5)
We know that the flux through $4\pi$ is given by$\dfrac{q}{{{\varepsilon }_{0}}}$, then, flux through ${{\Omega }_{1}}$ will be,
${{\phi }_{1}}=\dfrac{\dfrac{q}{{{\varepsilon }_{0}}}}{4\pi }2\pi \left( 1-\cos {{\theta }_{1}} \right)$
$\therefore {{\phi }_{1}}=\dfrac{q}{2{{\varepsilon }_{0}}}\left( 1-\cos {{\theta }_{1}} \right)$……………………… (6)
Similarly,
${{\phi }_{2}}=\dfrac{\dfrac{q}{{{\varepsilon }_{0}}}}{4\pi }2\pi \left( 1-\cos {{\theta }_{2}} \right)$
$\therefore {{\phi }_{2}}=\dfrac{q}{2{{\varepsilon }_{0}}}\left( 1-\cos {{\theta }_{2}} \right)$………………………….. (7)
Substituting (1), (6) and (7) in (2) we get,
$\phi =\dfrac{q}{{{\varepsilon }_{0}}}-\dfrac{q}{2{{\varepsilon }_{0}}}\left( 1-\cos {{\theta }_{1}}+1-\cos {{\theta }_{2}} \right)$
$\Rightarrow \phi =\dfrac{q}{{{\varepsilon }_{0}}}-\left( \dfrac{2q}{2{{\varepsilon }_{0}}} \right)-\dfrac{q}{2{{\varepsilon }_{0}}}\left( \cos {{\theta }_{1}}+\cos {{\theta }_{2}} \right)$
$\Rightarrow \phi =-\dfrac{q}{2{{\varepsilon }_{0}}}\left( \cos {{\theta }_{1}}+\cos {{\theta }_{2}} \right)$
Substituting (3) and (4), we get,
$\phi =-\dfrac{q}{2{{\varepsilon }_{0}}}\left( \dfrac{3}{\sqrt{10}}+\dfrac{1}{\sqrt{2}} \right)$
$\therefore \phi =-\dfrac{q}{2{{\varepsilon }_{0}}}\left( \dfrac{3+\sqrt{5}}{\sqrt{10}} \right)$
Therefore, we find the electric flux through the curved surface of the cylinder due to charge q to be,
$\phi =-\dfrac{q}{2{{\varepsilon }_{0}}}\left( \dfrac{3+\sqrt{5}}{\sqrt{10}} \right)$

Note: We know that electric flux is the measure of electric field through a surface. But we also know that the electric field itself doesn’t flow. So in reality, the electric flux is describing the electric field strength at any distance from the charge that is responsible for the field. It is also given by the expression,
$\phi =E\bullet S=ES\cos \theta$