Solveeit Logo
Login

Question

Question: A-5.(i) The cubical container ABCDEFGH which is completely filled with an ideal (nonviscous and inco...

A-5.(i) The cubical container ABCDEFGH which is completely filled with an ideal (nonviscous and incompressible) fluid, moves in a gravity free space with a acceleration of a = a0(i^−j^+k^)a_0(\hat{i}-\hat{j}+\hat{k}) where a0a_0 is a positive constant. Then the only point in the container shown in the figure where pressure is maximum, is

(ii) In previous question pressure will be minimum at point -

A

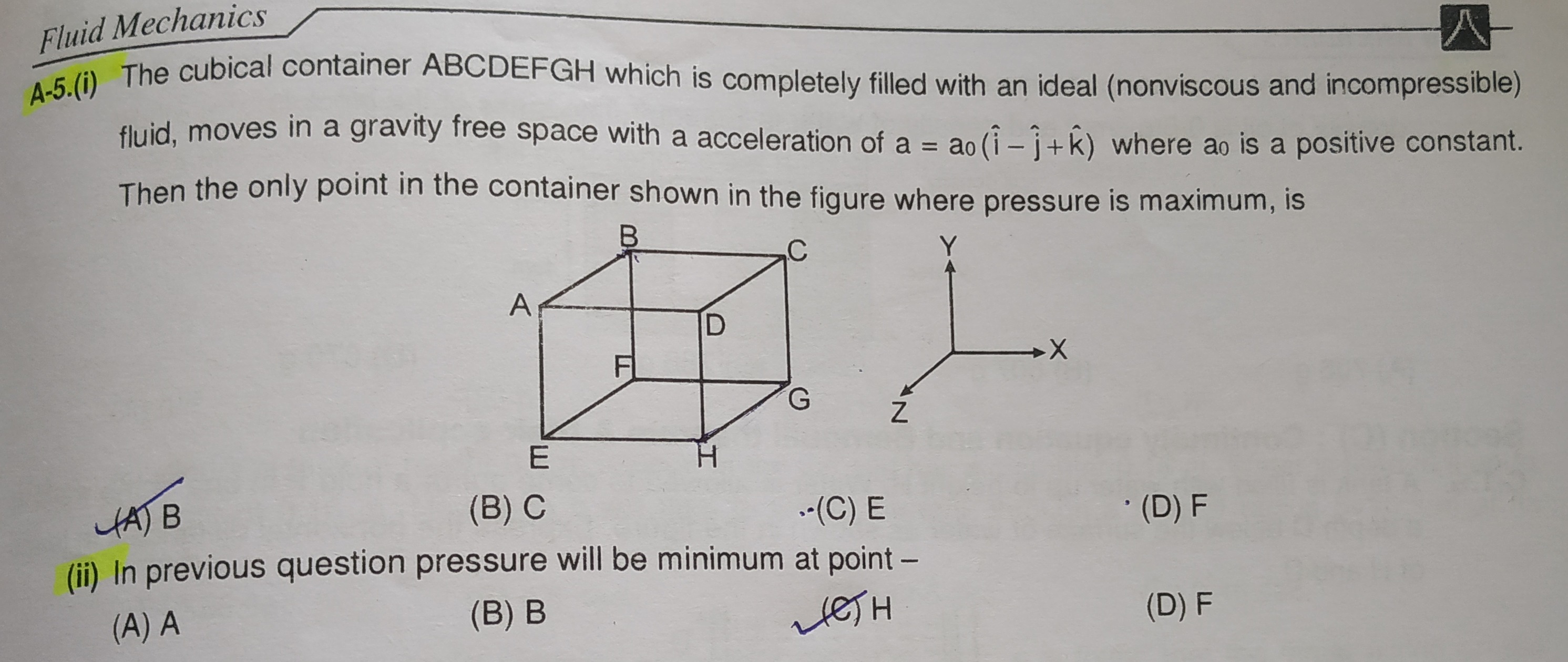
B

B

C

C

E

D

F

Answer

The maximum pressure is at point A, which is not listed in the options. Among the given options B and E have maximum pressure.

Explanation

Solution

The pressure variation in a fluid accelerating with acceleration a⃗\vec{a} in a gravity-free space is given by the equation:

∇P=−ρa⃗\nabla P = -\rho \vec{a}

This equation indicates that the pressure increases in the direction opposite to the acceleration vector a⃗\vec{a}. Conversely, the pressure decreases in the direction of the acceleration vector a⃗\vec{a}.

The given acceleration is a⃗=a0(i^−j^+k^)\vec{a} = a_0(\hat{i}-\hat{j}+\hat{k}), where a0a_0 is a positive constant. So, the direction of acceleration is (1,−1,1)(1, -1, 1).

To find the point of maximum pressure, we need to find the point that is farthest in the direction opposite to a⃗\vec{a}. The direction opposite to a⃗\vec{a} is −a⃗=a0(−i^+j^−k^)-\vec{a} = a_0(-\hat{i}+\hat{j}-\hat{k}).

The pressure at any point r⃗=(x,y,z)\vec{r}=(x,y,z) relative to a reference point (say, the origin E) can be written as:

P(r⃗)=PE−ρa⃗⋅r⃗P(\vec{r}) = P_E - \rho \vec{a} \cdot \vec{r}

To maximize P(r⃗)P(\vec{r}), we need to minimize the dot product a⃗⋅r⃗\vec{a} \cdot \vec{r}.

a⃗⋅r⃗=a0(i^−j^+k^)⋅(xi^+yj^+zk^)=a0(x−y+z)\vec{a} \cdot \vec{r} = a_0(\hat{i}-\hat{j}+\hat{k}) \cdot (x\hat{i}+y\hat{j}+z\hat{k}) = a_0(x-y+z).

So, we need to find the vertex (x,y,z)(x,y,z) for which the value of (x−y+z)(x-y+z) is minimum.

Let's define the coordinates of the vertices of the cube assuming E is at the origin (0,0,0) and the side length of the cube is LL. Based on the provided diagram with X, Y, Z axes:

  • E = (0, 0, 0)
  • H = (L, 0, 0)
  • F = (0, 0, L)
  • G = (L, 0, L)
  • A = (0, L, 0)
  • D = (L, L, 0)
  • B = (0, L, L)
  • C = (L, L, L)

Now, let's calculate (x−y+z)(x-y+z) for each vertex:

  • For E (0,0,0): 0−0+0=00 - 0 + 0 = 0
  • For H (L,0,0): L−0+0=LL - 0 + 0 = L
  • For F (0,0,L): 0−0+L=L0 - 0 + L = L
  • For G (L,0,L): L−0+L=2LL - 0 + L = 2L
  • For A (0,L,0): 0−L+0=−L0 - L + 0 = -L
  • For D (L,L,0): L−L+0=0L - L + 0 = 0
  • For B (0,L,L): 0−L+L=00 - L + L = 0
  • For C (L,L,L): L−L+L=LL - L + L = L

The minimum value of (x−y+z)(x-y+z) is −L-L, which occurs at point A. Therefore, the pressure is maximum at point A.

For Part (ii): Minimum Pressure

To find the point of minimum pressure, we need to maximize the dot product a⃗⋅r⃗\vec{a} \cdot \vec{r}, which means maximizing (x−y+z)(x-y+z).

The maximum value of (x−y+z)(x-y+z) is 2L2L, which occurs at point G. Therefore, the pressure is minimum at point G.