Question

Five rods of the same dimensions are arranged as shown. They have thermal conductivities ${k_1},{k_2},{k_3},{k_4}$and ${k_5}$. When points $A$ and $B$ are maintained at different temperatures, no heat flows through the central rod. It follows that: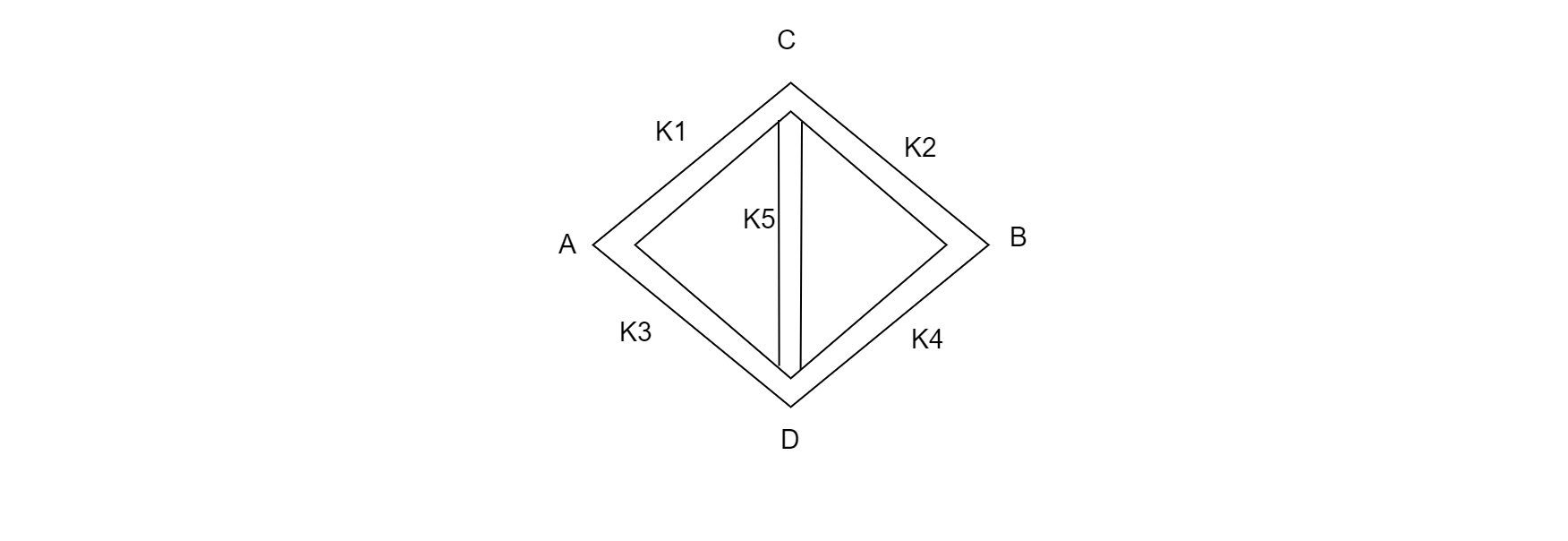
A) ${k_1} = {k_2}$ and ${k_2} = {k_3}$
B) ${k_1}/{k_4} = {k_2}/{k_3}$
C) ${k_1}{k_4} = {k_2}{k_3}$
D) ${k_1}{k_2} = {k_3}{k_4}$

Answer 1

The figure is analogous to the Wheatstone bridge in which an unknown resistance is calculated with the help of a bridge circuit. The Wheatstone bridge is used when the ratio of two resistances is equal to the other two resistances, then the voltage across the bridge will be zero.

Complete step by step solution:
We know that the thermal resistance $\left( R \right)$ is:
$R = \dfrac{L}{{KA}}$
Where $L$ is the length of the rod,
$K$ is the thermal conductivity coefficient of the rod,
$A$ is the area of the rod
Now we will apply the concept of Wheatstone bridge in which no current flows through the central rod because the ratio of two resistances is equal:
Therefore, ${R_1}{R_4} = {R_2}{R_3}$
Where ${R_1},{R_2},{R_3},{R_4}$ are the resistances for rods of thermal resistances ${k_1},{k_2},{k_3},{k_4}$ , respectively.
In the formula of thermal resistance, the term $\dfrac{L}{A}$ is a constant as all the rods are of the same dimensions as given in the question.
Therefore, $R \propto \dfrac{1}{K}$, so we get the following result:
$\Rightarrow {k_1}{k_4} = {k_2}{k_3}$

Therefore, option C is the correct option.

Additional information:
Wheatstone bridge was invented by Samuel Hunter Christie and was improved by Charles Wheatstone in the year $1843$. It was used for the analysis of soil. It can be used to measure the capacitance, inductance, impedance, etc., of a circuit. It is used to measure very small resistance values. It can also measure various other physical parameters such as temperature, strain, light, etc.

Note: The alternative method to solve is to consider that if no heat is passing through the central rod, then the temperature of the ends of the central rod will be the same. Therefore:
${k_1}\left( {{T_D} - {T_B}} \right) = {k_2}\left( {{T_C} - {T_B}} \right)$,
Since, ${T_c} = {T_D}$
we have, $\dfrac{{{k_1}}}{{{k_3}}} = \dfrac{{{k_2}}}{{{k_4}}}$
Therefore, ${k_1}{k_4} = {k_2}{k_3}$.