Question
Question: Five resistors are connected in a circuit as shown below. Find the ammeter reading when the circuit ...
Five resistors are connected in a circuit as shown below. Find the ammeter reading when the circuit is closed.
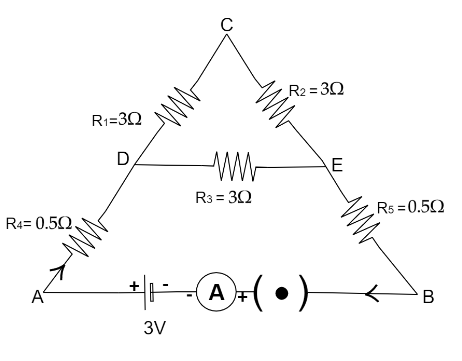
Solution
We have to solve this complicated circuit into a simplified one to get the current flowing through the ammeter. First solve the total resistance between DCE then calculate the total resistance between D and E, finally we can calculate the equivalent resistance and now with help of ohm’s law we can calculate the ammeter reading.
Complete step by step answer:
We have five resistance and are connected as shown below,
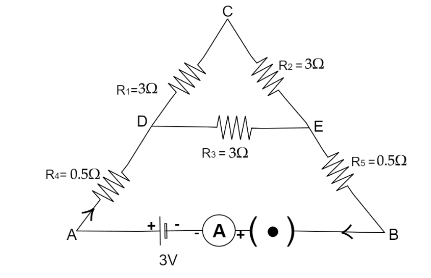
Now from the diagram we can see that resistance R1andR2 are connected in series in branch DCE,
R12=R1+R2
Now putting the known value we will get,
R12=3Ω+3Ω
⇒R12=6Ω
Now the equivalent circuit will look like,
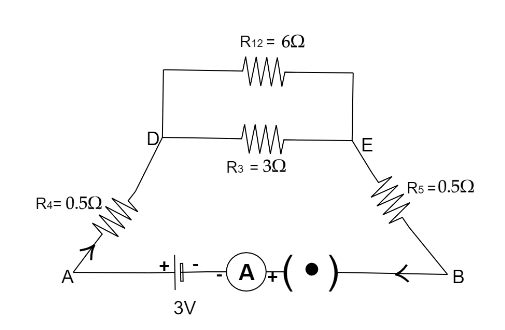
Now R12andR3 resistance are connected parallel in branch DE,
RDE=R12∣∣R3
We know, R=Ra∣∣Rb=Ra+RbRa×Rb
Now applying this formula in the above DE branch we will get,
RDE=R12+R3R12×R3
Now putting the known value we will get,
RDE=6Ω+3Ω6Ω×3Ω
⇒RDE=918Ω
Dividing the numerator and denominator by 9 we will get,
RDE=2Ω
Now the equivalent resistance will be,
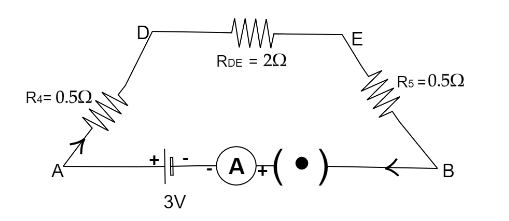
Now the equivalent resistance, from the above diagram R4,R5andRDE are connected in series. We will get,
\operatorname{R} {\text{eq = R_4 + }}R_{DE} + R5
Putting the known values in the above equation we will get,
Req = 0.5Ω + 2Ω+0.5Ω
⇒Req = 3Ω
Hence the equivalent resistance of the circuit is 3Ω.
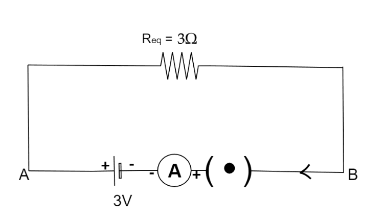
Ammeter: It is an instrument for measuring either direct or alternating electric current, in amperes.
For Ammeter Reading, applying Ohm’s Law we will get,
I=RV
Now putting the known value from the diagram we will get,
I=3Ω3V
∴I=1A
Hence the current reading in ammeter is 1A.
Note: Also while solving this kind of problem always draw the simplified circuit in each step so that you will not commit a mistake. We can solve this problem in many different ways. We can use the delta star method to open the circuit in a simplified version but for now we only know the envelope theory. In future classes you will come to know many other simplified methods to solve this kind of complicated circuit.
