Question

Five point charges, each of value $+ q$ are placed on five vertices of a regular hexagon of side L. What is the magnitude of the force on a point charge of value $- q$ placed at the centre of the hexagon?

Answer 1

Concept of electrostatic force of attraction between the charges and the charge at the centre of hexagon is to be used. Firstly individual electrostatic force of attraction between charge at each corner and center us to calculate which are then summed to find total force.

Complete step by step answer:
A regular Hexagon is given. Side of the Hexagon is ‘a’. Here $OA = OB = OC = OD = OE = OF = q.$Coulomb force (F) $= \dfrac{{K{q_1}{q_2}}}{{{r^2}}}$will be used. Here, ${q_1}\,and\,\,{q_2}$are ${r^2}$ charge and $r$ is the distance between both charges.

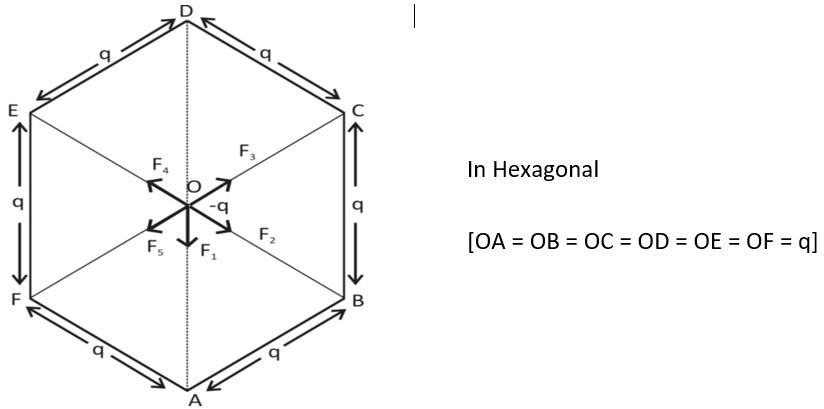
Now, five charges on vertices and at centre $- q$ charge is allocated. So positive charge at vertices and Negative charge at centre.

Attraction force applied
$\because$ Coulomb force: $F = \dfrac{{K{q_1}{q_2}}}{{{r^2}}}$
Here, five force at charge $- q$
{F_1} = \dfrac{{K{a^2}}}{{{a^2}}} [OA = a] \\\
{F_2} = \dfrac{{K{a^2}}}{{{a^2}}} \\\
{F_3} = \dfrac{{K{a^2}}}{{{a^2}}} \\\
{F_4} = \dfrac{{K{a^2}}}{{{a^2}}} \\\
{F_5} = \dfrac{{K{a^2}}}{{{a^2}}} \\\

Now, net force on point O
$\because {F_2} = {F_4}$(direction opposite)
${F_3} = {F_5}$ (direction opposite)
Net force $({F_2}\delta \,{F_4})\,and\,({F_3}\delta {F_5})$
F net $= 0$
Now, remain ${F_1}$force
${F_1} = \dfrac{{K{a^2}}}{{{a^2}}}$
Hence net force at point ‘O’ $= \dfrac{{K{a^2}}}{{{a^2}}}$
$\boxed{F{\,_{net}}\, = \dfrac{{K{a^2}}}{{{a^2}}}}$
Among the five forces due to five charges, $2$ pairs $({F_2}\delta \,{F_4})\,and\,({F_3}\delta {F_5})$are cancelled with each other since they are equal in magnitude and opposite in direction. The resultant force is due to a single force which is ${F_1}$
Hence, $\boxed{{F_1} = \dfrac{{K{a^2}}}{{{a^2}}}}$
$K = \dfrac{1}{{4\pi { \in _o}}}$
${F_1} = \dfrac{1}{{4\pi { \in _o}}}\dfrac{{{a^2}}}{{{a^2}}} { \in _o} =$ Permittivity of free space.

Note:
(i) Apply the concept of Coulomb force.
(ii) Concept of net force is used and attraction force is applied not that of repulsion because the charge at centre and at corners of the hexagon are of opposite polarity.
$\left[ {\overrightarrow {Fnet} = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} } \right]$