Question
Question: Five particles are situated on the corner of a regular pentagon as shown in figure. If one of the ma...
Five particles are situated on the corner of a regular pentagon as shown in figure. If one of the mass m will be replaced by 2m then what will be the shift in centre of mass?
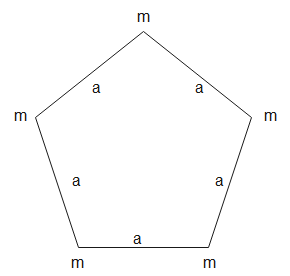
Solution
Centre of mass of a distributed mass system is an imaginary point where the whole mass of the system seems to be concentrated. Centre of mass is a unique point for a system. For regular shaped objects with uniform mass density, the centre of mass lies at centroid. When a mass is replaced by ‘2m’ the shift in centre of mass can be calculated using the formula of COM.
Formula used:
Coordinates of centre of mass, RCOM=M1i=1∑nmiri
Complete step by step answer:
Centre of mass of a system is defined as an imaginary point where the whole mass of the system seems to be concentrated. It is the balance point of the system. At this point, weighted position vectors of all the masses of a system adds to zero.
Mathematically, centre of mass for a system of particles is written as
RCOM=M1i=1∑nmiri
Where mi and ri are the mass and co-ordinates of particle i respectively. M is the total mass of the whole system.
Initially, the situation is as shown in figure. As the system is regularly shaped with uniform distribution of masses, therefore, the centroid of pentagon coincides with the centre of mass of the system. Let us assume that the centroid of the system coincides with the origin of the coordinate system. Now, the system can be imagined to be concentrated at origin having mass ‘5m’.
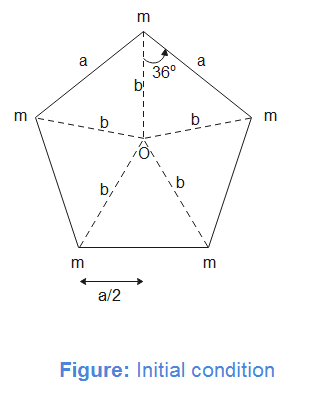
When one mass ‘m’ is replaced with ‘2m’, the mass at one of the vertices increases by ‘m’ or more precisely one extra mass ‘m’ is placed at the vertex. Therefore, the new centre of mass is
RCOM=6m5m×0+m×b=6b
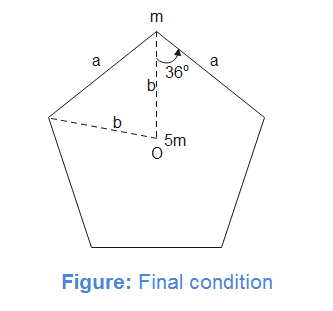
Centroid of a regular pentagon of edge length ‘a’ is at distance acos36∘ from its vertices. Therefore, b=acos36∘=0.809a
The new centre of mass is at distance 6b from the centroid. Therefore, the shift in centre of mass is
ΔRCOM=6b=60.809a=0.135a
Note:
For regular shaped objects with uniform mass density, the centre of mass lies at centroid. This statement may not be true for objects with non-uniform density. For objects whose dimensions are much smaller than the radius of earth, the centre of mass and centre of gravity coincide. Centre of mass lies near the heavier portion of a system.
