Question
Question: Five identical strings are used in the following three configurations. The time periods of vertical ...
Five identical strings are used in the following three configurations. The time periods of vertical oscillations in the following configuration are in ratio:
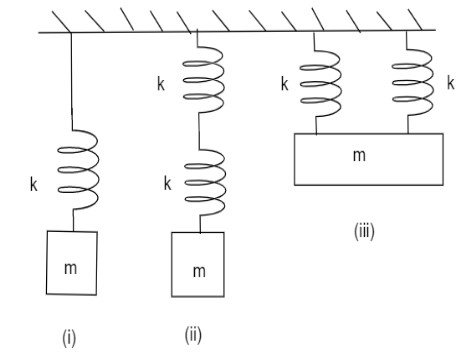
A. 1 : 2 : 21
B. 2 : 2 : 21
C. 21 : 2 : 1
D. 2 : 21 : 1
Solution
We will find the time period of oscillation of the spring in each case. Also when two springs are attached in parallel or series combination then we have to calculate the equivalent spring constant. Thus we will find an equivalent spring constant before finding the time period of oscillations.
Formula Used:
(i) T = 2πkm
(ii) For parallel combination of springs:
keq. = k1 + k2 + ...............kn
(iii) For series combination of springs:
keq.1 = k11 + k21 + ...............kn1
Complete step by step answer:
The time taken by the spring to complete one vertical oscillation is known as the time period of vertical oscillations. It depends on the spring constant k and mass of the body (m) attached to it. The time period to complete one vertical oscillation is given by:
T = 2πkm
When two or more springs are attached to each other in series combination or parallel combination then we have to calculate the equivalent spring constant of the system and the formula reduced as,
T = 2πkeq.m
Time period for figure (i):
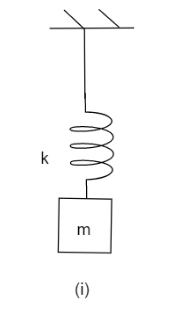
The time period for above system can be written as:
T(i) = 2πkm
Time period for figure (ii)
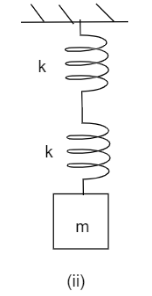
Here two ideal springs of spring constant k each are attached in series combination with mass (m). Therefore we will find the equivalent spring constant for above system as,
For series combination:
keq.1 = k11 + k21 + ...............kn1
Here k1 and k2 both are equal to k. Thus on substituting values we get keq. as:
keq.1 = k11 + k21
⇒keq.1 = k1 + k1
⇒keq.1 = k2
⇒keq. = 2k
Now the time period for the given system will be calculated as:
T(ii) = 2πkeq.m
⇒ T(ii) = 2π2km
⇒ T(ii) = 2πk2m
Time period for figure (iii)
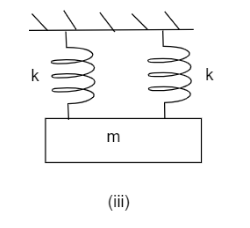
Here two identical springs of spring constant k are joined in a parallel combination. Therefore the equivalent spring constant can be calculated as:
For parallel combination:
keq. = k1 + k2 + ...............kn
Here k1 and k2 both are equal to k. Thus on substituting values we get keq. as:
⇒keq. = k1 + k2
⇒keq. = k + k
⇒keq. = 2k
Time period of vertical oscillation will be equal to:
T(iii) = 2πkeq.m
⇒ T(iii) = 2π2km
Now we will find the ratio of T(i) : T(ii) : T(iii) and get the result as:
T(i) : T(ii) : T(iii) = 2πkm : 2πk2m : 2π2km
∴T(i) : T(ii) : T(iii) = 1: 2 : 21
Hence the correct option is A.
Note: Before finding the time period of oscillation we must ensure to find the equivalent spring constant of the system. The concept used for finding equivalent spring constant is the reverse of that of equivalent combination of resistance. Also the mass we used is reduced mass.
