Question

Five identical capacitor plates, each of area $A$, are arranged such that adjacent plates are at a distance $d$ apart; the plates are connected to a source of emf $V$ as shown in the figure.

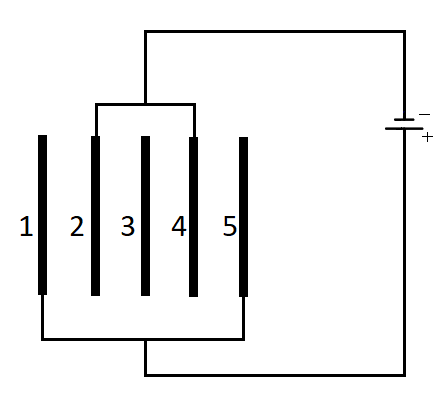
Charge on plate 1 is _______ and plate 4 is________

Answer 1

Hint
By considering the arrangement as capacitors, we can find the charge on the first plate as the charge is the product of the capacitance and the voltage. For the fourth capacitor, it is between 2 other plates so it will have twice the amount of charge on it.

Formula Used: In this solution we will be using the following formula,
$Q = CV$
where $Q$ is the charge,
$C$ is the capacitance and $V$ is the voltage.

Complete step by step answer
To solve this problem we will be considering the arrangement as that of 4 capacitors. Now as it is given that the distance between the plates is $d$ and the area of each os the plate is $A$. So the capacitance of each of the plates will be
$C = \dfrac{{{\varepsilon _o}A}}{d}$
Now for the first plate it is connected across the positive terminal of the battery. Do the voltage across it would be positive. The emf of the battery is given to be $V$. So the potential across the first plate will be $+ V$.
Therefore the charge on the first capacitor plate will be given by the formula, $Q = CV$. So substituting the values of the capacitance and the voltage we will get,
$Q = + \dfrac{{{\varepsilon _o}A}}{d}V$
Now, for the fourth plate, we can see from the diagram that the fourth plate is placed in between 2 plates. So the charge on it will be twice the amount. Now the fourth plate can be seen from the diagram as attached to the negative terminal of the battery. So the potential across the fourth plate will be $- V$. Since the capacitance of all the plates are the same, the capacitance across the fourth plate is $C = \dfrac{{{\varepsilon _o}A}}{d}$. Therefore, the charge across the fourth plate will be given by the formula, $Q = CV$. So substituting we get,
$Q = 2 \times \dfrac{{{\varepsilon _o}A}}{d}\left( { - V} \right)$
The 2 is present due to the 2 plates on either side of the fourth plate.
So we get,
$Q = - \dfrac{{2{\varepsilon _o}A}}{d}V$
Therefore, charge on plate 1 is $+ \dfrac{{{\varepsilon _o}A}}{d}V$ and plate 4 is $- \dfrac{{2{\varepsilon _o}A}}{d}V$.

Note
A capacitor is a device that stores electrical energy in an electric field. In an electrical circuit, when 2 conductors are kept in proximity to one another, then it is called a capacitor. The presence of a capacitor adds capacitance to a circuit.