Question
Question: Five equal resistors each of resistance \[R\] are connected as shown in the adjoining figure. A batt...
Five equal resistors each of resistance R are connected as shown in the adjoining figure. A battery of V volt is connected between A and B. the current flowing in AFCEB will be:
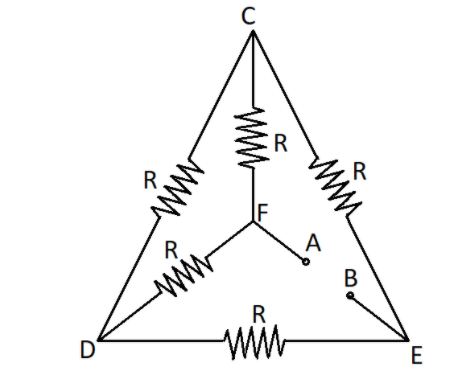
(A) R3V
(B) RV
(C) 2RV
(D) R2V
Solution
The equivalent circuit can be drawn as a wheatstone bridge. The total current flowing in a wheatstone bridge when all resistances are equal is simply the voltage over the value of the resistance.
Formula used: In this solution we will be using the following formulae;
V=IR where V is the voltage or potential difference across a resistor, I is the current through the resistor, and R is the resistance value of the resistor.
Complete Step-by-Step solution:
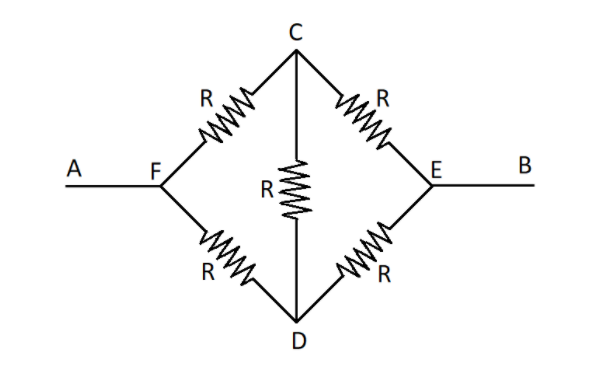
Given a circuit and told to calculate the current through a section of the circuit. To solve this, observe that the circuit can be drawn equivalently to the more recognized version of the wheatstone bridge as shown in the figure.
Generally, in a wheatstone bridge, the ratio of the resistances at the left of the dividing resistor (i.e. the resistor at the middle connecting one arm of the bridge to the other) to that of the right of the dividing resistor. In this case, since all resistances are equal, the ratio is equal to one.
Also, in this case, the voltage across the middle resistor will be equal to zero. Then the total current flowing through bridge is given by
I=RV where V is the voltage or potential difference across a resistor, and R is the resistance value of the resistor.
Hence, the current flowing through one section AFCEB of the bridge is Is=2RV
Hence, the correct option is C
Note: For clarity, the equivalent resistance in the circuit is equal to the resistance of one resistor in a wheatstone bridge. That is why, the effective current flowing in the entire circuit is given from\
I=ReqV as
I=RV (since Req=R)
