Question
Question: Five circuits are shown below. All the batteries have the same voltage \( V \) and all resistors hav...
Five circuits are shown below. All the batteries have the same voltage V and all resistors have the same resistance R . In which circuit does the battery deliver the most power?
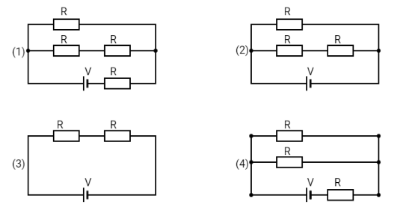
Solution
Hint : Joule's law, which states that the heat emitted in resistance is proportional to the square of the current flowing through the resistance over a given time, is directly related to Ohm's law.
Complete Step By Step Answer:
The difference in charge between two points is known as voltage. The rate at which charge flows is referred to as current. The inclination of a substance to resist the movement of charge is known as resistance (current).
We know that Power=V×I where V represents the applied voltage and I represents the current in the circuit.
According to Ohm ’s Law, we know that IV=R
We can rewrite it as I=RV
Now we substitute I in the formula of power. So, we get,
Power = V \times I = V \times \dfrac{V}{R} \\\
\therefore Power = \dfrac{{{V^2}}}{R} \\\
We have to find which battery delivers the most power, from the above equation it is obvious that power will be the most when resistance is the least.
Considering option 1 :
Resistance in parallel is,
\dfrac{1}{{{R_P}}} = \left( {\dfrac{1}{R} + \dfrac{1}{{2R}}} \right) \\\
\Rightarrow \dfrac{1}{{{R_P}}} = \dfrac{3}{{2R}} \\\
\Rightarrow \dfrac{1}{{{R_P}}} = \dfrac{3}{{2R}} \\\
\Rightarrow {R_P} = \dfrac{{2R}}{3} \\\
RS=R
Total resistance is, RT=RP+RS
RT=32R+R=35R
Considering option 2 :
Resistance in parallel is,
\dfrac{1}{{{R_P}}} = \left( {\dfrac{1}{R} + \dfrac{1}{{2R}}} \right) \\\
\Rightarrow \dfrac{1}{{{R_P}}} = \dfrac{3}{{2R}} \\\
\Rightarrow \dfrac{1}{{{R_P}}} = \dfrac{3}{{2R}} \\\
\Rightarrow {R_P} = \dfrac{{2R}}{3} \\\
RS=0
Total resistance is, RT=RP+RS
RT=32R+0=32R
Considering option 3 :
Resistance in parallel is,
\dfrac{1}{{{R_P}}} = 0 \\\
\Rightarrow {R_P} = 0 \\\
RS=R+R=2R
Total resistance is, RT=RP+RS
RT=0+2R=2R
Considering option 4 :
Resistance in parallel is,
\dfrac{1}{{{R_P}}} = \left( {\dfrac{1}{R} + \dfrac{1}{R}} \right) \\\
\Rightarrow \dfrac{1}{{{R_P}}} = \dfrac{2}{R} \\\
\Rightarrow {R_P} = \dfrac{R}{2} \\\
RS=R
Total resistance is, RT=RP+RS
RT=2R+R=23R
Since option 2 has the least resistance, RT=32R .
Therefore, option 2 circuit’s battery delivers the most power.
Note :
In electrical systems, resistance is a critical property that can be calculated. Ohms are the units used to assess resistance. Low-resistance materials allow electricity to flow freely. To allow electricity flow through materials with higher resistance, more voltage (EMF) is required.
